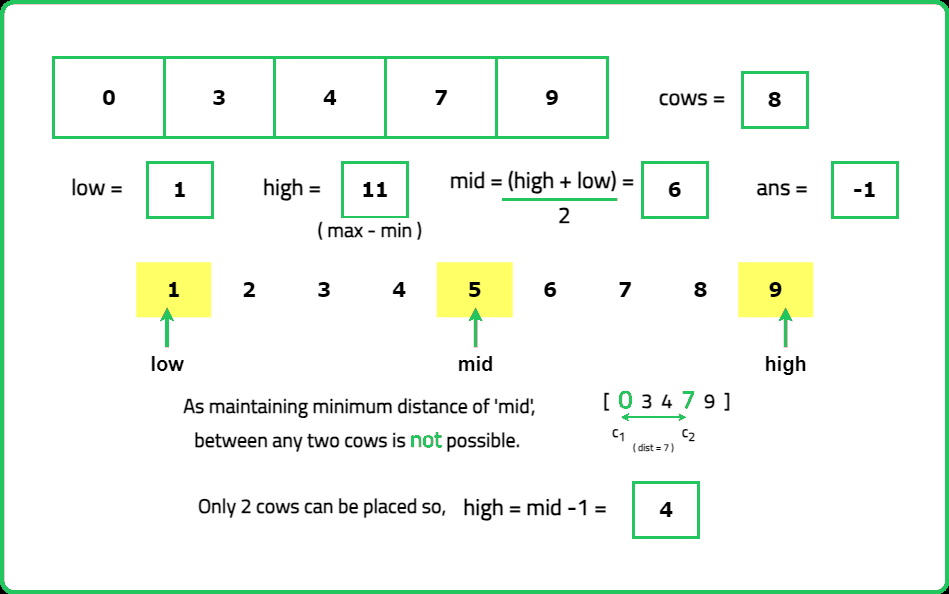
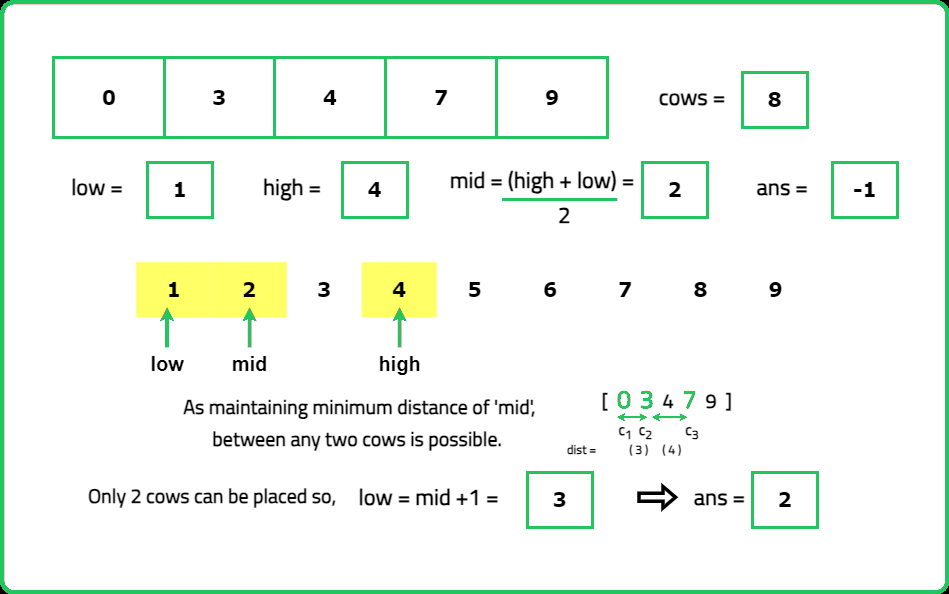
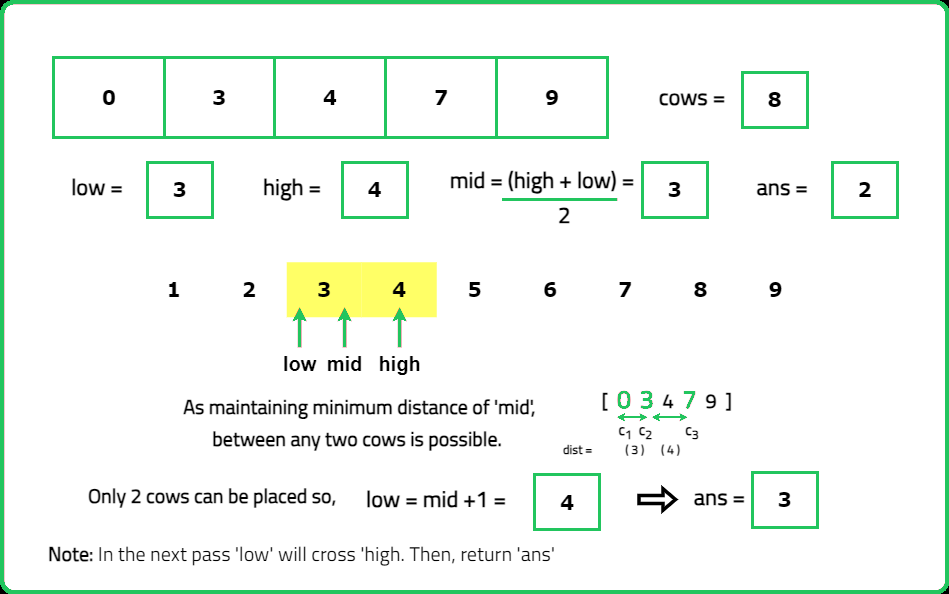
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071
#include <bits/stdc++.h>
using namespace std;
class Solution {
private:
/* Function to check if we can place 'cows' cows
with at least 'dist' distance apart in 'stalls' */
bool canWePlace(vector<int> &nums, int dist, int cows) {
// Size of array
int n = nums.size();
// Number of cows placed
int cntCows = 1;
// Position of last placed cow
int last = nums[0];
for (int i = 1; i < n; i++) {
if (nums[i] - last >= dist) {
// Place next cow
cntCows++;
// Update the last location
last = nums[i];
}
if (cntCows >= cows) return true;
}
return false;
}
public:
/* Function to find the maximum possible minimum
distance 'k' cows can have between them in 'stalls' */
int aggressiveCows(vector<int> &nums, int k) {
// Size of array
int n = nums.size();
// Sort the nums
sort(nums.begin(), nums.end());
int low = 1, high = nums[n - 1] - nums[0];
//Apply binary search:
while (low <= high) {
int mid = (low + high) / 2;
if (canWePlace(nums, mid, k) == true) {
low = mid + 1;
}
else high = mid - 1;
}
return high;
}
};
int main() {
vector<int> nums = {0, 3, 4, 7, 10, 9};
int k = 4;
// Create an instance of the Solution class
Solution sol;
int ans = sol.aggressiveCows(nums, k);
// Output the result
cout << "The maximum possible minimum distance is: " << ans << "\n";
return 0;
}
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263
import java.util.Arrays;
class Solution {
/* Function to check if we can place 'cows' cows
with at least 'dist' distance apart */
private boolean canWePlace(int[] nums, int dist, int cows) {
// Size of array
int n = nums.length;
// Number of cows placed
int cntCows = 1;
// Position of last placed cow
int last = nums[0];
for (int i = 1; i < n; i++) {
if (nums[i] - last >= dist) {
// Place next cow
cntCows++;
// Update the last location
last = nums[i];
}
if (cntCows >= cows) return true;
}
return false;
}
/* Function to find the maximum possible minimum
distance 'k' cows can have between them in nums */
public int aggressiveCows(int[] nums, int k) {
// Size of array
int n = nums.length;
// Sort the nums
Arrays.sort(nums);
int low = 1, high = nums[n - 1] - nums[0];
//Apply binary search:
while (low <= high) {
int mid = (low + high) / 2;
if (canWePlace(nums, mid, k) == true) {
low = mid + 1;
}
else high = mid - 1;
}
return high;
}
public static void main(String[] args) {
int[] nums = {0, 3, 4, 7, 10, 9};
int k = 4;
// Create an instance of the Solution class
Solution sol = new Solution();
int ans = sol.aggressiveCows(nums, k);
// Output the result
System.out.println("The maximum possible minimum distance is: " + ans);
}
}
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556
class Solution:
"""Function to check if we can place 'cows'
cows with at least 'dist' distance apart"""
def canWePlace(self, nums, dist, cows):
# Size of array
n = len(nums)
# Number of cows placed
cntCows = 1
# Position of last placed cow
last = nums[0]
for i in range(1, n):
if nums[i] - last >= dist:
# Place next cow
cntCows += 1
# Update the last location
last = nums[i]
if cntCows >= cows:
return True
return False
""" Function to find the maximum possible minimum
distance 'k' cows can have between them in 'nums'"""
def aggressiveCows(self, nums, k):
# Size of array
n = len(nums)
# Sort the nums
nums.sort()
low = 1
high = nums[n - 1] - nums[0]
# Apply binary search
while low <= high:
mid = (low + high) // 2
if self.canWePlace(nums, mid, k):
low = mid + 1
else:
high = mid - 1
return high
if __name__ == "__main__":
nums = [0, 3, 4, 7, 10, 9]
k = 4
# Create an instance of the Solution class
sol = Solution()
ans = sol.aggressiveCows(nums, k)
# Output the result
print("The maximum possible minimum distance is:", ans)
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566
class Solution {
/* Function to check if we can place 'cows'
cows with at least 'dist' distance apart */
canWePlace(nums, dist, cows) {
// Size of array
let n = nums.length;
// Number of cows placed
let cntCows = 1;
// Position of last placed cow
let last = nums[0];
for (let i = 1; i < n; i++) {
if (nums[i] - last >= dist) {
// Place next cow
cntCows++;
// Update the last location
last = nums[i];
}
if (cntCows >= cows) return true;
}
return false;
}
/* Function to find the maximum possible minimum
distance 'k' cows can have between them in 'nums' */
aggressiveCows(nums, k) {
// Size of array
let n = nums.length;
// Sort the nums
nums.sort((a, b) => a - b);
let low = 1, high = nums[n - 1] - nums[0];
// Apply binary search
while (low <= high) {
const mid = Math.floor((low + high) / 2);
if (this.canWePlace(nums, mid, k)) {
low = mid + 1;
} else {
high = mid - 1;
}
}
//Return the answer
return high;
}
}
function main() {
let nums = [0, 3, 4, 7, 10, 9];
let k = 4;
// Create an instance of the Solution class
let sol = new Solution();
let ans = sol.aggressiveCows(nums, k);
// Output the result
console.log("The maximum possible minimum distance is:", ans);
}
// Call the main function
main();