Count partitions with given difference
Dynamic Programming
DP on subsequences
Hard
Given an array arr of n integers and an integer diff, count the number of ways to partition the array into two subsets such that the absolute difference between their sums is equal to diff. Return the result modulo 109+7.
Examples:
Input: arr = [1, 1, 2, 3], diff = 1
Output: 3
Explanation: The subsets are [1, 2] and [1, 3], [1, 3] and [1, 2], [1, 1, 2] and [3].
Input: arr = [1, 2, 3, 4], diff = 2
Output: 2
Explanation: The subsets are [1, 3] and [2, 4], [1, 2, 3] and [4].
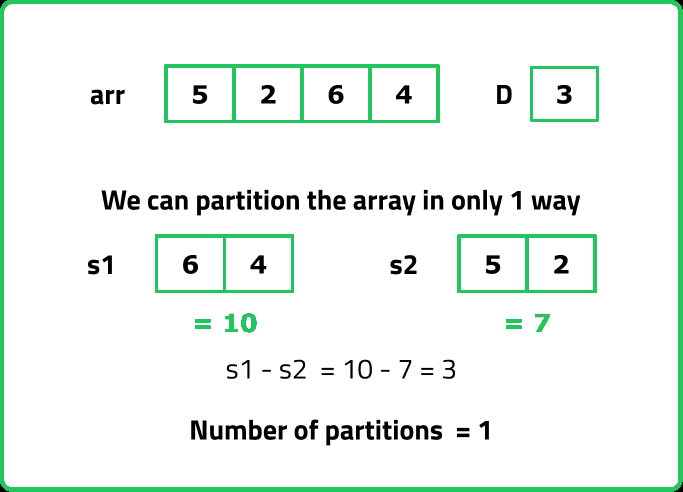
Input: arr = [5, 2, 6, 4], diff = 3
Constraints
- 1 <= n <= 200
- 0 <= d <= 104
- 0 <= arr[i] <= 50
Hints
- "the problem reduces to finding the number of subsets whose sum is S1. If S + diff is odd, no valid partition exists → return 0. Otherwise, find count of subsets that sum to S1 using Subset Sum Count DP."
- We use a 1D DP array (dp[j]) where dp[j] represents the number of ways to achieve sum j. We iterate in reverse (j = S1 to arr[i]) to avoid duplicate counting.
Company Tags
Zoho
Teladoc Health
Ernst & Young
Roblox
KPMG
Epic Games
Databricks
Deloitte
Instacart
Intel
Seagate Technology
Micron Technology
Electronic Arts
Docker
Rakuten
Goldman Sachs
Snowflake
Medtronic
Philips Healthcare
JPMorgan Chase
Unity Technologies
Boston Consulting Group
Ubisoft
Walmart
Square
Google
Microsoft
Amazon
Meta
Apple
Netflix
Adobe
Editorial
Understanding:
This article will be divided into two parts:
First, we will discuss an extra edge case of the problem discussed in Count Subsets with Sum K, and then, we will discuss the problem for this article: Partitions with Given Difference.
- Part 1: Extra edge case for the problem Count Subsets with Sum K
- Part 2: Count Partitions with Given Difference.
In the problem Count Subsets with Sum K, the problem constraints stated that an array element is greater than 0, so the code we have written there works perfectly for the given constraints.
If the constraints mentioned that an array element can also be equal to 0 and the target sum can also be 0, then that code will fail. To understand it we will take an example:
Let the target arr = [0,0,1] and the target = 1.
The previous code will give us the answer 1 as it first takes the element arr[2] and then finds the answer by picking it. Then from the base condition, we will return 0 ( as the target will become 0 by picking 1). But for this question, the answer will be 4 with the following subsets({0,1},{0,1},{0,0,1} and {1}).
Therefore we need to modify the base conditions in order to handle the changes. These are the base conditions of that problem.
1234
f(ind, target){
if(target == 0) return 1
if(ind == 0) return arr[ind] == target
}First of all, we will remove target==0 because now when target ==0, there can be many 0s present in the array which needs to be counted in the answer.
1234
f(ind, target){
if(ind == 0) return arr[ind] == target
}Now, the following cases can arise when we are at index 0, if the target sum is 0 and the first index is also 0, like in case [0,1], we can form the subset in two ways, either by considering the first element or leaving it, so we can return 2.
1234
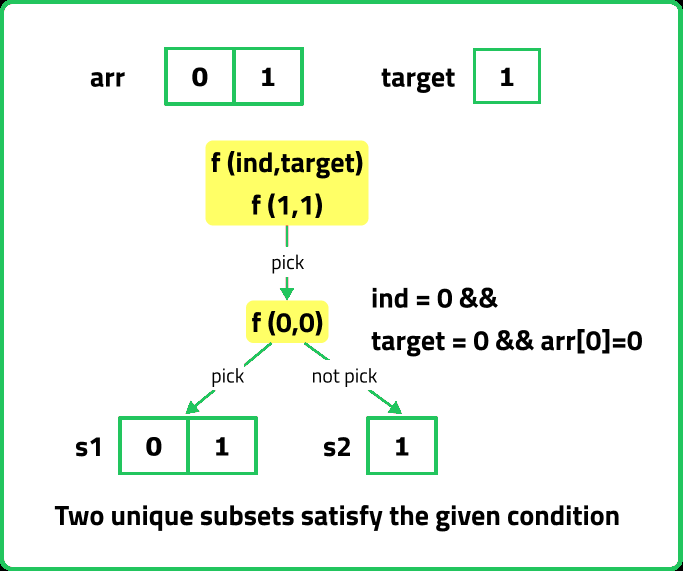
f(ind, target){
if(ind == 0) {
if(target == 0 && arr[0] == 0)
return 2
}
}Else at index 0, if target == 0, and the first element is not 0, it means we will not pick the first element so we just return 1 way.
1234
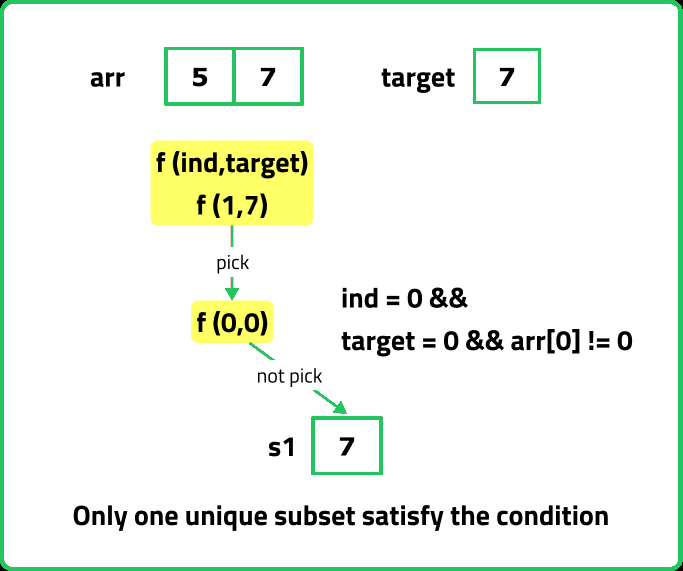
f(ind, target){
if(ind == 0) {
if(target == 0 && arr[0] == 0)
return 2
if(target == 0)
return 1
}
}Or if at index 0, when the first element is not 0, and the target is equal to the first element , then we will include it in the subset and we will return 1 way.
1234
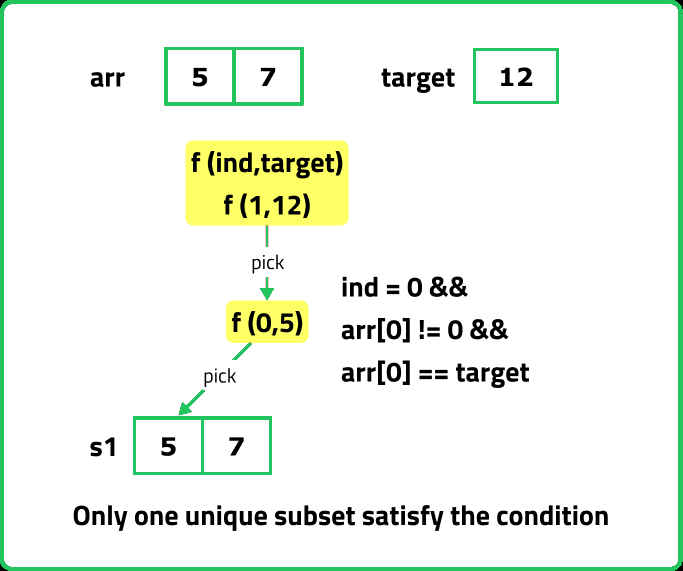
f(ind, target){
if(ind == 0) {
if(target == 0 && arr[0] == 0)
return 2
if(target == 0 || arr[0] == target)
return 1
}
}Else in all other cases, we simply return 0.
This question is a slight modification of the problem discussed in "Count Subsets with Sum K". We have the following two conditions given to us.
S1 + S2 = D – (i)
S1 >= S2 – (ii)
If we calculate the total sum of elements of the array (say totSum), we can say that,
S1 = totSum - S2 – (iii)
Now solving for equations (i) and (iii), we can say that
S2 = (totSum - D)/2 – (iv)
Therefore the question “Count Partitions with a difference D” is modified to “Count Number of subsets with sum (totSum - D)/2 ”. This is exactly what we had discussed in the article "Count Subsets with Sum K".
The following edge cases need to be handled:
As the array elements are positive integers including zero, we don’t want to find the case when S2 is negative or we can say that totSum is lesser than D, therefore if totSum
Steps to form the recursive solution:
- Express the problem in terms of indexes: The array will have an index but there is one more parameter “target”. We are given the initial problem to find whether there exists in the whole array a subsequence whose sum is equal to the target.
- Try out all possible choices at a given index:We have two choices:
- Return the sum of taken and notTaken: As we have to return the total count of subsets with the target sum, we will return the sum of taken and notTaken from our recursive call.
- Base Cases: If target == 0, it means that we have already found the subsequence from the previous steps, so we can return 1. If ind==0, it means we are at the first element, so we need to return arr[ind]==target. If the element is equal to the target we return 1 else we return 0.
So, we can say that initially, we need to find(n-1, target) which means that we are counting the number of subsequences in the array from index 0 to n-1, whose sum is equal to the target.
Exclude the current element from the subsequence: We first try to find a subsequence without considering the current index element. For this, we will make a recursive call to f(ind-1, target).
Include the current element in the subsequence: We will try to find a subsequence by considering the current index as an element as part of the subsequence. As we have included arr[ind], the updated target which we need to find in the rest of the array will be a target - arr[ind]. Therefore, we will call f(ind-1,target-arr[ind]).
1234
f(ind, target){
notTaken = f(ind-1, target)
taken = 0
if(arr[ind] <= target)
taken = f(ind-1, target-arr[ind])
}Note: We will consider the current element in the subsequence only when the current element is less than or equal to the target.
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283
#include <bits/stdc++.h>
using namespace std;
class Solution {
// Modulus value to avoid overflow in calculations.
int mod = (int)1e9 + 7;
public:
/* Recursive function to count the number of subsets
with a given target sum. Uses memoization to store results
of subproblems to avoid redundant computations. */
int countPartitionsUtil(int ind, int target, vector<int>& arr) {
// Base case: If we are at the first element.
if (ind == 0) {
/* If target is 0 and the element is also 0,there
are 2 ways to achieve this (include or exclude).*/
if (target == 0 && arr[0] == 0)
return 2;
/* If target is 0 or the element is equal to
target, there is 1 way to achieve this*/
if (target == 0 || target == arr[0])
return 1;
return 0;
}
/* Calculate the number of ways not
including the current element.*/
int notTaken = countPartitionsUtil(ind - 1, target, arr);
/* Calculate the number of ways including the
current element (if it can be included).*/
int taken = 0;
if (arr[ind] <= target)
taken = countPartitionsUtil(ind - 1, target - arr[ind], arr);
// Return the result
return (notTaken + taken) % mod;
}
public:
/* Function to count number of subsets with a
given difference.Uses the helper function
`countPartitionsUtil` to find the number of subsets
with a specific target sum. */
int countPartitions(int n, int diff, vector<int>& arr) {
int totSum = 0;
// Calculate the total sum of elements in the array.
for (int i = 0; i < arr.size(); i++) {
totSum += arr[i];
}
/* If the total sum minus the difference is negative,
or if it is not even, it's not possible to divide
the array into two subsets with the given difference.*/
if (totSum - diff < 0) return 0;
if ((totSum - diff) % 2 == 1) return 0;
// Calculate the target sum for one of the subsets.
int s2 = (totSum - diff) / 2;
/* Call the helper function to count
the number of subsets with sum s2.*/
return countPartitionsUtil(n - 1, s2, arr);
}
};
int main() {
vector<int> arr = {5, 2, 6, 4};
int n = arr.size();
int diff = 3;
// Create an instance of Solution class
Solution sol;
// Print the number of subsets found
cout << "The number of subsets found are " << sol.countPartitions(n, diff, arr) << endl;
return 0;
}
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576
import java.util.*;
class Solution {
// Modulus value to avoid overflow in calculations.
int mod = (int)1e9 + 7;
/* Recursive function to count the number of subsets
with a given target sum. Uses memoization to store results
of subproblems to avoid redundant computations. */
int countPartitionsUtil(int ind, int target, int[] arr) {
// Base case: If we are at the first element.
if (ind == 0) {
/* If target is 0 and the element is also 0, there
are 2 ways to achieve this (include or exclude). */
if (target == 0 && arr[0] == 0)
return 2;
/* If target is 0 or the element is equal to
target, there is 1 way to achieve this. */
if (target == 0 || target == arr[0])
return 1;
return 0;
}
// Calculate number of ways not including current element.
int notTaken = countPartitionsUtil(ind - 1, target, arr);
/* Calculate the number of ways including the
current element (if it can be included). */
int taken = 0;
if (arr[ind] <= target)
taken = countPartitionsUtil(ind - 1, target - arr[ind], arr);
// Return the result
return (notTaken + taken) % mod;
}
/* Function to count number of subsets with a given
difference.Uses the helper function `countPartitionsUtil`
to find the number of subsets with a specific target sum. */
int countPartitions(int n, int diff, int[] arr) {
int totSum = 0;
// Calculate the total sum of elements in the array.
for (int i = 0; i < arr.length; i++) {
totSum += arr[i];
}
/* If the total sum minus the difference is negative,
or if it is not even, it's not possible to divide
the array into two subsets with the given difference. */
if (totSum - diff < 0) return 0;
if ((totSum - diff) % 2 == 1) return 0;
// Calculate the target sum for one of the subsets.
int s2 = (totSum - diff) / 2;
/* Call the helper function to count
the number of subsets with sum s2. */
return countPartitionsUtil(n - 1, s2, arr);
}
public static void main(String[] args) {
int[] arr = {5, 2, 6, 4};
int n = arr.length;
int diff = 3;
// Create an instance of Solution class
Solution sol = new Solution();
// Print the number of subsets found
System.out.println("The number of subsets found are " + sol.countPartitions(n, diff, arr));
}
}
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455
class Solution:
# Modulus value to avoid overflow in calculations.
mod = int(1e9 + 7)
def countPartitionsUtil(self, ind, target, arr):
# Base case: If we are at the first element.
if ind == 0:
""" If target is 0 and element is also 0, there
are 2 ways to achieve this (include or exclude)."""
if target == 0 and arr[0] == 0:
return 2
""" If target is 0 or the element is equal to
target, there is 1 way to achieve this."""
if target == 0 or target == arr[0]:
return 1
return 0
# Calculate number of ways not including current element.
not_taken = self.countPartitionsUtil(ind - 1, target, arr)
""" Calculate the number of ways including
the current element (if it can be included)."""
taken = 0
if arr[ind] <= target:
taken = self.countPartitionsUtil(ind - 1, target - arr[ind], arr)
# Return the result
return (not_taken + taken) % self.mod
def countPartitions(self, n, diff, arr):
tot_sum = sum(arr)
"""If the total sum minus the difference is negative,
or if it is not even, it's not possible to divide
the array into two subsets with the given difference."""
if tot_sum - diff < 0 or (tot_sum - diff) % 2 == 1:
return 0
# Calculate the target sum for one of the subsets.
s2 = (tot_sum - diff) // 2
""" Call the helper function to count
the number of subsets with sum s2."""
return self.countPartitionsUtil(n - 1, s2, arr)
arr = [5, 2, 6, 4]
n = len(arr)
diff = 3
# Create an instance of Solution class
sol = Solution()
# Print the number of subsets found
print(f"The number of subsets found are {sol.countPartitions(n, diff, arr)}")
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869
class Solution {
// Modulus value to avoid overflow in calculations.
constructor() {
this.mod = 1e9 + 7;
}
/* Recursive function to count the number of subsets
with a given target sum. Uses memoization to store results
of subproblems to avoid redundant computations. */
countPartitionsUtil(ind, target, arr) {
// Base case: If we are at the first element.
if (ind === 0) {
/* If target is 0 and the element is also 0,
there are 2 ways to achieve this */
if (target === 0 && arr[0] === 0)
return 2;
/* If target is 0 or the element is equal
to target, there is 1 way to achieve this.*/
if (target === 0 || target === arr[0])
return 1;
return 0;
}
// Calculate number of ways not including current element.
const notTaken = this.countPartitionsUtil(ind - 1, target, arr);
/* Calculate the number of ways including the
current element (if it can be included).*/
let taken = 0;
if (arr[ind] <= target)
taken = this.countPartitionsUtil(ind - 1, target - arr[ind], arr);
// Return the result
return (notTaken + taken) % this.mod;
}
/* Function to count the number of subsets with a
given difference.Uses the helper function
'countPartitionsUtil` to find the number of subsets
with a specific target sum. */
countPartitions(n, diff, arr) {
let totSum = arr.reduce((sum, num) => sum + num, 0);
/* If the total sum minus the difference is negative,
or if it is not even, it's not possible to divide
the array into two subsets with the given difference.*/
if (totSum - diff < 0 || (totSum - diff) % 2 === 1)
return 0;
// Calculate the target sum for one of the subsets.
let s2 = (totSum - diff) / 2;
// Call the helper function to count the number of subsets with sum s2.
return this.countPartitionsUtil(n - 1, s2, arr);
}
}
let arr = [5, 2, 6, 4];
let n = arr.length;
let diff = 3;
// Create an instance of Solution class
let sol = new Solution();
// Print the number of subsets found
console.log(`The number of subsets found are ${sol.countPartitions(n, diff, arr)}`);
Complexity Analysis:
Time Complexity:O(2N), As there are 2 choices for each index.Space Complexity:O(N), As we are using recursion stack of depth N.
If we draw the recursion tree, we will see that there are overlapping subproblems. Hence the DP approaches can be applied to the recursive solution.
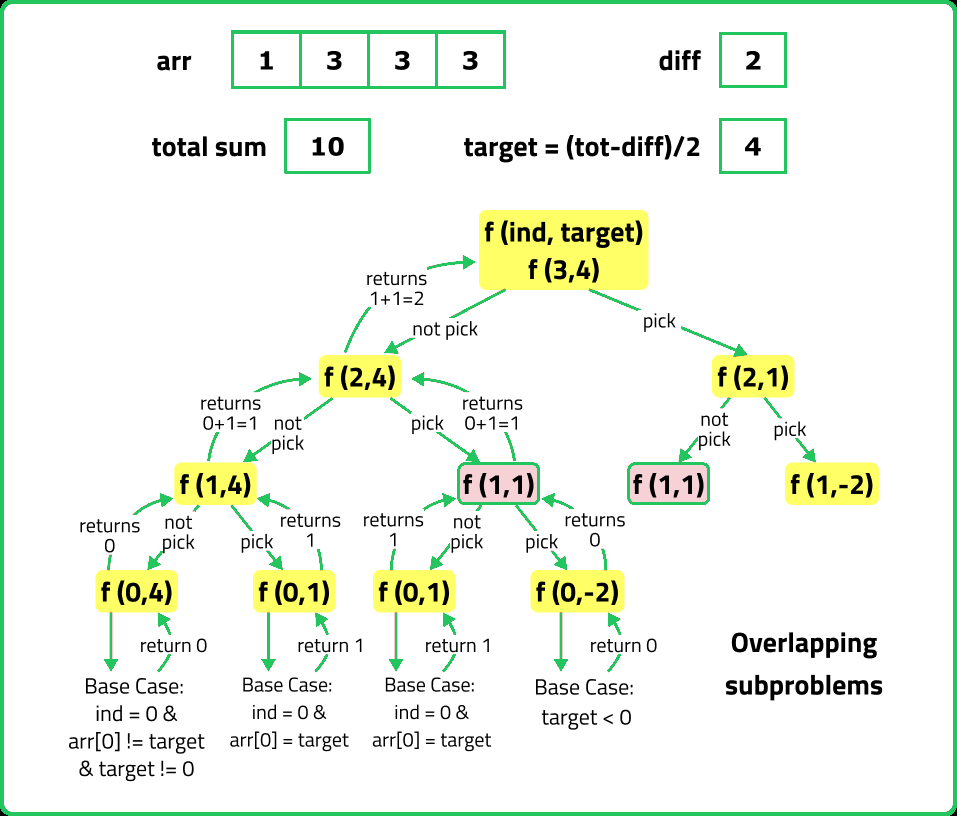
In order to convert a recursive solution to memoization the following steps will be taken:
- Declare a dp array of size [n][k+1]: As there are two changing parameters in the recursive solution, 'ind' and 'k'. The maximum value 'ind' can attain is (n-1){0 to n-1}, where n is the size of array and for 'k' only values from 0 to k is possible. Therefore, we need 2D dp array.
- While encountering an overlapping subproblem: When we come across a subproblem, for which the dp array has value other than -1, it means we have found a subproblem which has been solved before hence it is an overlapping subproblem. No need to calculate it's value again just retrieve the value from dp array and return it.
- Store the value of subproblem: Whenever, a subproblem is enocountered and it is not solved yet(the value at this index will be -1 in the dp array), store the calculated value of subproblem in the array.
The dp array stores the calculations of subproblems. Initialize dp array with -1, to indicate that no subproblem has been solved yet.
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576777879808182838485868788899091
#include <bits/stdc++.h>
using namespace std;
class Solution {
// Modulus value to avoid overflow in calculations.
int mod = (int)1e9 + 7;
public:
/* Recursive function to count the number of subsets
with a given target sum. Uses memoization to store results
of subproblems to avoid redundant computations. */
int countPartitionsUtil(int ind, int target, vector<int>& arr, vector<vector<int>> &dp) {
// Base case: If we are at the first element.
if (ind == 0) {
/* If target is 0 and the element is also 0,there
are 2 ways to achieve this (include or exclude).*/
if (target == 0 && arr[0] == 0)
return 2;
/* If target is 0 or the element is equal to
target, there is 1 way to achieve this*/
if (target == 0 || target == arr[0])
return 1;
return 0;
}
// Return the result if it has already been computed.
if (dp[ind][target] != -1)
return dp[ind][target];
/* Calculate the number of ways not
including the current element.*/
int notTaken = countPartitionsUtil(ind - 1, target, arr, dp);
/* Calculate the number of ways including the
current element (if it can be included).*/
int taken = 0;
if (arr[ind] <= target)
taken = countPartitionsUtil(ind - 1, target - arr[ind], arr, dp);
/* Store and return the result
for the current subproblem.*/
return dp[ind][target] = (notTaken + taken) % mod;
}
public:
/* Function to count number of subsets with a
given difference.Uses the helper function
`countPartitionsUtil` to find the number of subsets
with a specific target sum. */
int countPartitions(int n, int diff, vector<int>& arr) {
int totSum = 0;
// Calculate the total sum of elements in the array.
for (int i = 0; i < arr.size(); i++) {
totSum += arr[i];
}
/* If the total sum minus the difference is negative,
or if it is not even, it's not possible to divide
the array into two subsets with the given difference.*/
if (totSum - diff < 0) return 0;
if ((totSum - diff) % 2 == 1) return 0;
// Calculate the target sum for one of the subsets.
int s2 = (totSum - diff) / 2;
// Initialize the DP table with -1 for memoization.
vector<vector<int>> dp(n, vector<int>(s2 + 1, -1));
/* Call the helper function to count
the number of subsets with sum s2.*/
return countPartitionsUtil(n - 1, s2, arr, dp);
}
};
int main() {
vector<int> arr = {5, 2, 6, 4};
int n = arr.size();
int diff = 3;
// Create an instance of Solution class
Solution sol;
// Print the number of subsets found
cout << "The number of subsets found are " << sol.countPartitions(n, diff, arr) << endl;
return 0;
}
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848586
import java.util.*;
class Solution {
// Modulus value to avoid overflow in calculations.
int mod = (int)1e9 + 7;
/* Recursive function to count the number of subsets
with a given target sum. Uses memoization to store results
of subproblems to avoid redundant computations. */
int countPartitionsUtil(int ind, int target, int[] arr, int[][] dp) {
// Base case: If we are at the first element.
if (ind == 0) {
/* If target is 0 and the element is also 0, there
are 2 ways to achieve this (include or exclude). */
if (target == 0 && arr[0] == 0)
return 2;
/* If target is 0 or the element is equal to
target, there is 1 way to achieve this. */
if (target == 0 || target == arr[0])
return 1;
return 0;
}
// Return the result if it has already been computed.
if (dp[ind][target] != -1)
return dp[ind][target];
// Calculate number of ways not including current element.
int notTaken = countPartitionsUtil(ind - 1, target, arr, dp);
/* Calculate the number of ways including the
current element (if it can be included). */
int taken = 0;
if (arr[ind] <= target)
taken = countPartitionsUtil(ind - 1, target - arr[ind], arr, dp);
// Store and return the result for current subproblem.
return dp[ind][target] = (notTaken + taken) % mod;
}
/* Function to count number of subsets with a given
difference.Uses the helper function `countPartitionsUtil`
to find the number of subsets with a specific target sum. */
int countPartitions(int n, int diff, int[] arr) {
int totSum = 0;
// Calculate the total sum of elements in the array.
for (int i = 0; i < arr.length; i++) {
totSum += arr[i];
}
/* If the total sum minus the difference is negative,
or if it is not even, it's not possible to divide
the array into two subsets with the given difference. */
if (totSum - diff < 0) return 0;
if ((totSum - diff) % 2 == 1) return 0;
// Calculate the target sum for one of the subsets.
int s2 = (totSum - diff) / 2;
// Initialize the DP table with -1 for memoization.
int[][] dp = new int[n][s2 + 1];
for (int[] row : dp) {
Arrays.fill(row, -1);
}
/* Call the helper function to count
the number of subsets with sum s2. */
return countPartitionsUtil(n - 1, s2, arr, dp);
}
public static void main(String[] args) {
int[] arr = {5, 2, 6, 4};
int n = arr.length;
int diff = 3;
// Create an instance of Solution class
Solution sol = new Solution();
// Print the number of subsets found
System.out.println("The number of subsets found are " + sol.countPartitions(n, diff, arr));
}
}
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263
class Solution:
# Modulus value to avoid overflow in calculations.
mod = int(1e9 + 7)
def countPartitionsUtil(self, ind, target, arr, dp):
# Base case: If we are at the first element.
if ind == 0:
""" If target is 0 and element is also 0, there
are 2 ways to achieve this (include or exclude)."""
if target == 0 and arr[0] == 0:
return 2
""" If target is 0 or the element is equal to
target, there is 1 way to achieve this."""
if target == 0 or target == arr[0]:
return 1
return 0
# Return the result if it has already been computed.
if dp[ind][target] != -1:
return dp[ind][target]
# Calculate number of ways not including current element.
not_taken = self.countPartitionsUtil(ind - 1, target, arr, dp)
""" Calculate the number of ways including
the current element (if it can be included)."""
taken = 0
if arr[ind] <= target:
taken = self.countPartitionsUtil(ind - 1, target - arr[ind], arr, dp)
# Store and return the result for the current subproblem.
dp[ind][target] = (not_taken + taken) % self.mod
return dp[ind][target]
def countPartitions(self, n, diff, arr):
tot_sum = sum(arr)
"""If the total sum minus the difference is negative,
or if it is not even, it's not possible to divide
the array into two subsets with the given difference."""
if tot_sum - diff < 0 or (tot_sum - diff) % 2 == 1:
return 0
# Calculate the target sum for one of the subsets.
s2 = (tot_sum - diff) // 2
# Initialize the DP table with -1 for memoization.
dp = [[-1 for _ in range(s2 + 1)] for _ in range(n)]
""" Call the helper function to count
the number of subsets with sum s2."""
return self.countPartitionsUtil(n - 1, s2, arr, dp)
arr = [5, 2, 6, 4]
n = len(arr)
diff = 3
# Create an instance of Solution class
sol = Solution()
# Print the number of subsets found
print(f"The number of subsets found are {sol.countPartitions(n, diff, arr)}")
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677
class Solution {
// Modulus value to avoid overflow in calculations.
constructor() {
this.mod = 1e9 + 7;
}
/* Recursive function to count the number of subsets
with a given target sum. Uses memoization to store results
of subproblems to avoid redundant computations. */
countPartitionsUtil(ind, target, arr, dp) {
// Base case: If we are at the first element.
if (ind === 0) {
/* If target is 0 and the element is also 0,
there are 2 ways to achieve this */
if (target === 0 && arr[0] === 0)
return 2;
/* If target is 0 or the element is equal
to target, there is 1 way to achieve this.*/
if (target === 0 || target === arr[0])
return 1;
return 0;
}
// Return the result if it has already been computed.
if (dp[ind][target] !== -1)
return dp[ind][target];
// Calculate the number of ways not including current element.
const notTaken = this.countPartitionsUtil(ind - 1, target, arr, dp);
/* Calculate the number of ways including the
current element (if it can be included).*/
let taken = 0;
if (arr[ind] <= target)
taken = this.countPartitionsUtil(ind - 1, target - arr[ind], arr, dp);
// Store and return the result for current subproblem.
dp[ind][target] = (notTaken + taken) % this.mod;
return dp[ind][target];
}
/* Function to count the number of subsets with a
given difference.Uses the helper function
'countPartitionsUtil` to find the number of subsets
with a specific target sum. */
countPartitions(n, diff, arr) {
let totSum = arr.reduce((sum, num) => sum + num, 0);
/* If the total sum minus the difference is negative,
or if it is not even, it's not possible to divide
the array into two subsets with the given difference.*/
if (totSum - diff < 0 || (totSum - diff) % 2 === 1)
return 0;
// Calculate the target sum for one of the subsets.
let s2 = (totSum - diff) / 2;
// Initialize the DP table with -1 for memoization.
let dp = Array.from({ length: n }, () => Array(s2 + 1).fill(-1));
// Call the helper function to count the number of subsets with sum s2.
return this.countPartitionsUtil(n - 1, s2, arr, dp);
}
}
let arr = [5, 2, 6, 4];
let n = arr.length;
let diff = 3;
// Create an instance of Solution class
let sol = new Solution();
// Print the number of subsets found
console.log(`The number of subsets found are ${sol.countPartitions(n, diff, arr)}`);
Complexity Analysis:
Time Complexity: O(N*K), There are 'N*K' states therefore at max ‘N*K’ new problems will be solved.Space Complexity:O(N*K) + O(N), As we are using a recursion stack space(O(N)) and a 2D array ( O(N*K)).
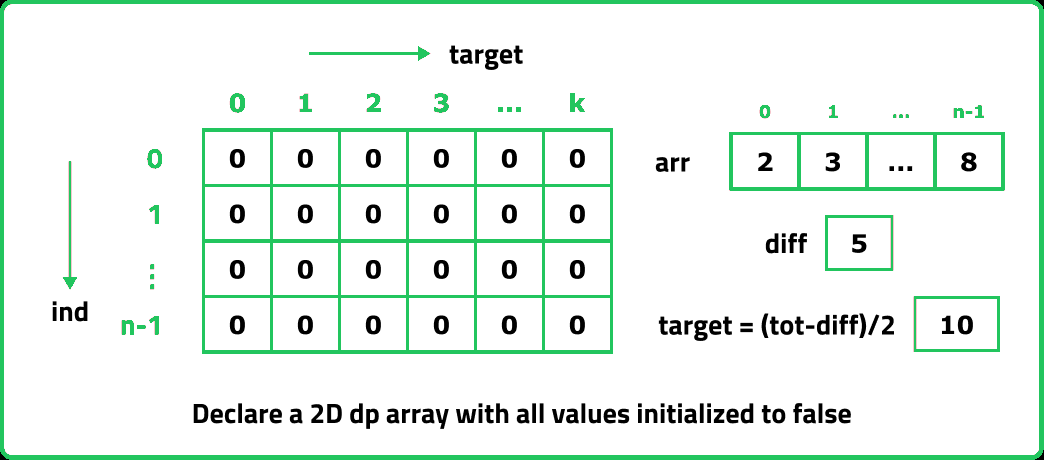
In order to convert a recursive code to tabulation code, we try to convert the recursive code to tabulation and here are the steps:
- Declare a dp array of size [n][k+1]: As there are two changing parameters in the recursive solution, 'ind' and 'k'. The maximum value 'ind' can attain is (n-1){0 to n-1}, where n is the size of array and for 'k' only values from 0 to k is possible. Therefore, we need 2D dp array.
- Setting Base Cases in the Array: In the recursive code, our base condition was when target == 0. If target == 0, 'ind' can take any value from 0 to n-1, therefore we need to set the value of the first column as 1.
- Iterative Computation Using Loops: Initialize two nested for loops to traverse the dp array and following the logic discussed in the recursive approach, set the value of each cell in the 2D dp array. Instead of recursive calls, use the dp array itself to find the values of intermediate calculations.
- Returning the answer: At last dp[n-1][k] will hold the solution after the completion of whole process, as we are doing the calculations in bottom-up manner.
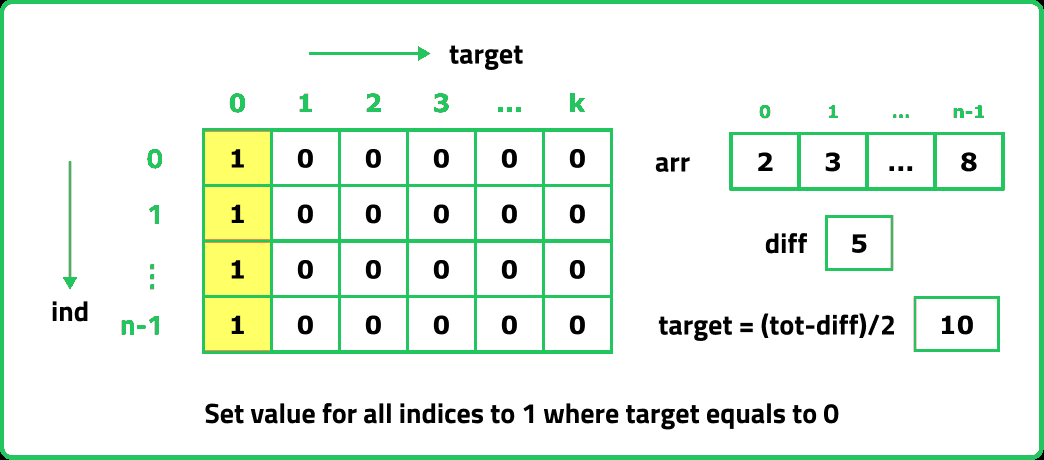
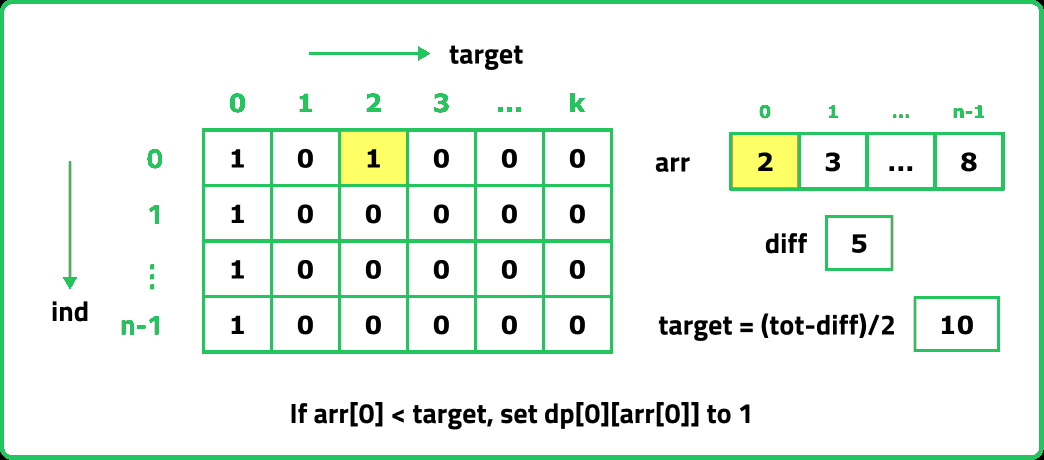
The first row dp[0][] indicates that only the first element of the array is considered, therefore for the target value equal to arr[0], only cell with that target will be true, so explicitly set dp[0][arr[0]] =1, (dp[0][arr[0]] means that we are considering the first element of the array with the target equal to the first element itself). Please note that it can happen that arr[0]>target, so we first check it: if(arr[0]<=target) then set dp[0][arr[0]] = 1
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687
#include <bits/stdc++.h>
using namespace std;
class Solution {
// Modulus value to avoid overflow in calculations.
int mod = (int)1e9 + 7;
private:
/* Function to calculate the number of ways to
achieve a target sum with the given numbers.*/
int findWays(vector<int> &num, int tar) {
int n = num.size();
/* DP table where dp[i][j] represents the number
of ways to get sum j using the first i elements.*/
vector<vector<int>> dp(n, vector<int>(tar + 1, 0));
/* If the first element is 0, we have 2
ways to achieve sum 0: by either including
or excluding the element.*/
if (num[0] == 0) dp[0][0] = 2;
else dp[0][0] = 1;
/* If the first element is not 0 and is less
than or equal to target, we have 1 way to
achieve the sum equal to that element.*/
if (num[0] != 0 && num[0] <= tar) dp[0][num[0]] = 1;
// Fill the DP table for the rest of the elements.
for (int ind = 1; ind < n; ind++) {
for (int target = 0; target <= tar; target++) {
/* Number of ways to achieve target sum
without using the current element.*/
int notTaken = dp[ind - 1][target];
/* Number of ways to achieve target
sum using the current element.*/
int taken = 0;
if (num[ind] <= target)
taken = dp[ind - 1][target - num[ind]];
/* Total ways to achieve target sum with
or without including the current element.*/
dp[ind][target] = (notTaken + taken) % mod;
}
}
/* Return the number of ways to achieve
the target sum using all elements.*/
return dp[n - 1][tar];
}
public:
/* Function to count the number of
subsets with a given difference.*/
int countPartitions(int n, int diff, vector<int>& arr) {
int totSum = 0;
// Calculate the total sum of elements in the array.
for (int i = 0; i < n; i++) {
totSum += arr[i];
}
/* If the difference is more than the total sum or
if the difference is not even (as (totalSum - diff)
must be even to divide into two subsets), return 0.*/
if (totSum - diff < 0 || (totSum - diff) % 2) return 0;
/* Call the helper function to find the number
of subsets with sum (totSum - diff) / 2.*/
return findWays(arr, (totSum - diff) / 2);
}
};
int main() {
vector<int> arr = {5, 2, 6, 4};
int n = arr.size();
int diff = 3;
// Create an instance of Solution class
Solution sol;
// Print the number of subsets found
cout << "The number of subsets found are " << sol.countPartitions(n, diff, arr) << endl;
return 0;
}
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576777879808182
import java.util.*;
class Solution {
// Modulus value to avoid overflow in calculations.
private static final int MOD = (int)1e9 + 7;
/* Function to calculate the number of ways to
achieve a target sum with the given numbers.*/
private int findWays(int[] num, int tar) {
int n = num.length;
/* DP table where dp[i][j] represents the number
of ways to get sum j using the first i elements.*/
int[][] dp = new int[n][tar + 1];
/* If the first element is 0, we have 2
ways to achieve sum 0: by either including
or excluding the element.*/
if (num[0] == 0) dp[0][0] = 2;
else dp[0][0] = 1;
/* If the first element is not 0 and is less
than or equal to target, we have 1 way to
achieve the sum equal to that element.*/
if (num[0] != 0 && num[0] <= tar) dp[0][num[0]] = 1;
// Fill the DP table for the rest of the elements.
for (int ind = 1; ind < n; ind++) {
for (int target = 0; target <= tar; target++) {
/* Number of ways to achieve target sum
without using the current element.*/
int notTaken = dp[ind - 1][target];
/* Number of ways to achieve target
sum using the current element.*/
int taken = 0;
if (num[ind] <= target)
taken = dp[ind - 1][target - num[ind]];
/* Total ways to achieve target sum with
or without including the current element.*/
dp[ind][target] = (notTaken + taken) % MOD;
}
}
/* Return the number of ways to achieve
the target sum using all elements.*/
return dp[n - 1][tar];
}
/* Function to count the number of
subsets with a given difference.*/
public int countPartitions(int n, int diff, int[] arr) {
int totSum = 0;
// Calculate the total sum of elements in the array.
for (int i = 0; i < n; i++) {
totSum += arr[i];
}
/* If the difference is more than the total sum or
if the difference is not even (as (totalSum - diff)
must be even to divide into two subsets), return 0.*/
if (totSum - diff < 0 || (totSum - diff) % 2 != 0) return 0;
/* Call the helper function to find the number
of subsets with sum (totSum - diff) / 2.*/
return findWays(arr, (totSum - diff) / 2);
}
public static void main(String[] args) {
int[] arr = {5, 2, 6, 4};
int n = arr.length;
int diff = 3;
// Create an instance of Solution class
Solution sol = new Solution();
// Print the number of subsets found
System.out.println("The number of subsets found are " + sol.countPartitions(n, diff, arr));
}
}
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071
MOD = int(1e9 + 7)
class Solution:
""" Function to calculate the number of ways to
achieve a target sum with the given numbers."""
def findWays(self, num, tar):
n = len(num)
""" DP table where dp[i][j] represents the number
of ways to get sum j using the first i elements."""
dp = [[0] * (tar + 1) for _ in range(n)]
""" If the first element is 0, we have 2
ways to achieve sum 0: by either including
or excluding the element."""
if num[0] == 0:
dp[0][0] = 2
else:
dp[0][0] = 1
""" If the first element is not 0 and is less
than or equal to target, we have 1 way to
achieve the sum equal to that element."""
if num[0] != 0 and num[0] <= tar:
dp[0][num[0]] = 1
# Fill the DP table for the rest of the elements.
for ind in range(1, n):
for target in range(tar + 1):
""" Number of ways to achieve target sum
without using the current element."""
not_taken = dp[ind - 1][target]
""" Number of ways to achieve target
sum using the current element."""
taken = 0
if num[ind] <= target:
taken = dp[ind - 1][target - num[ind]]
""" Total ways to achieve target sum with
or without including the current element."""
dp[ind][target] = (not_taken + taken) % MOD
""" Return the number of ways to achieve
the target sum using all elements."""
return dp[n - 1][tar]
""" Function to count the number of
subsets with a given difference."""
def countPartitions(self, n, diff, arr):
tot_sum = sum(arr)
""" If the difference is more than the total sum
or if the difference is not even, return 0."""
if tot_sum - diff < 0 or (tot_sum - diff) % 2 != 0:
return 0
""" Call the helper function to find the number
of subsets with sum (tot_sum - diff) / 2."""
return self.findWays(arr, (tot_sum - diff) // 2)
if __name__ == "__main__":
arr = [5, 2, 6, 4]
n = len(arr)
diff = 3
# Create an instance of Solution class
sol = Solution()
# Print the number of subsets found
print("The number of subsets found are", sol.countPartitions(n, diff, arr))
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172
const MOD = 1e9 + 7;
class Solution {
/* Function to calculate the number of ways to
achieve a target sum with the given numbers.*/
findWays(num, tar) {
const n = num.length;
/* DP table where dp[i][j] represents the number
of ways to get sum j using the first i elements.*/
const dp = Array.from({ length: n }, () => Array(tar + 1).fill(0));
/* If the first element is 0, we have 2
ways to achieve sum 0: by either including
or excluding the element.*/
if (num[0] === 0) dp[0][0] = 2;
else dp[0][0] = 1;
/* If the first element is not 0 and is less
than or equal to target, we have 1 way to
achieve the sum equal to that element.*/
if (num[0] !== 0 && num[0] <= tar) dp[0][num[0]] = 1;
// Fill the DP table for the rest of the elements.
for (let ind = 1; ind < n; ind++) {
for (let target = 0; target <= tar; target++) {
/* Number of ways to achieve target
sum without using the current element.*/
const notTaken = dp[ind - 1][target];
/* Number of ways to achieve target
sum using the current element.*/
let taken = 0;
if (num[ind] <= target)
taken = dp[ind - 1][target - num[ind]];
/* Total ways to achieve target sum with
or without including the current element.*/
dp[ind][target] = (notTaken + taken) % MOD;
}
}
/* Return the number of ways to achieve
the target sum using all elements.*/
return dp[n - 1][tar];
}
/* Function to count the number of
subsets with a given difference.*/
countPartitions(n, diff, arr) {
const totSum = arr.reduce((a, b) => a + b, 0);
/* If the difference is more than the total
sum or if the difference is not even, return 0.*/
if (totSum - diff < 0 || (totSum - diff) % 2 !== 0)
return 0;
/* Call the helper function to find the number
of subsets with sum (totSum - diff) / 2.*/
return this.findWays(arr, (totSum - diff) / 2);
}
}
const arr = [5, 2, 6, 4];
const n = arr.length;
const diff = 3;
// Create an instance of Solution class
const sol = new Solution();
// Print the number of subsets found
console.log("The number of subsets found are", sol.countPartitions(n, diff, arr));
Complexity Analysis:
Time Complexity: O(N*K), As, here are three nested loops that account for O(N*K) complexity.Space Complexity:O(N*K), As a 2D array of size N*K is used.
If we observe the relation, dp[ind][target] = dp[ind-1][target] + dp[ind-1][target-arr[ind]]. We find that to calculate a value of a cell of the dp array, we need only the previous row values (say prev). So, we don’t need to store an entire array. Hence we can space optimize it.
Steps to space optimize the tabulation approach:
- Decalre an array of size target to store the previous row of the DP table. Initialize the first row and first column of the DP table based on the base conditions discussed in tabulation.
- Now, initiate two nested loops in bottom-up approach. The first loop will run for 'ind' and the second loop will run for the 'target' variable.
- In order to store the current row of the DP table, initialize a new array 'cur' and fill the first cell to 1 for base condition.
- Do the calculations for 'cur' row by performing the pick/non-pick technique used in previous approaches.
- Now, update the previous row with the current row for the next iteration and at last return the final result stored in the last cell of the previous row(prev[k]).
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848586878889909192
#include <bits/stdc++.h>
using namespace std;
class Solution {
// Modulus value to avoid overflow in calculations.
int mod = (int)1e9 + 7;
private:
/* Function to calculate the number of subsets
with a specific target sum. Uses space optimization
to store only the previous state in the DP table. */
int findWays(vector<int> &num, int tar) {
int n = num.size();
/* DP table to store number of ways
to achieve a certain target sum.*/
vector<int> prev(tar + 1, 0);
/* 2 cases for target 0 when the first
element is 0: either pick it or not.*/
if (num[0] == 0) prev[0] = 2;
/* 1 case for target 0 when the first
element is non-zero: just don't pick it.*/
else prev[0] = 1;
/* Initialize the base case for the
first element and non-zero target.*/
if (num[0] != 0 && num[0] <= tar) prev[num[0]] = 1;
/* Iterate through all elements of the
array starting from the second element.*/
for (int ind = 1; ind < n; ind++) {
vector<int> cur(tar + 1, 0);
for (int target = 0; target <= tar; target++) {
/* Number of ways to achieve the target
sum without including the current element.*/
int notTaken = prev[target];
/* Number of ways to achieve the target sum
by including the current element.*/
int taken = 0;
if (num[ind] <= target)
taken = prev[target - num[ind]];
/* Total ways to achieve the target sum either
including or excluding the current element.*/
cur[target] = (notTaken + taken) % mod;
}
/* Update the previous state to the current
state for the next iteration.*/
prev = cur;
}
// Return the number of subsets
return prev[tar];
}
public:
/* Function to count the number of subsets with a
given difference.Uses the helper function findWays
to find number of subsets with a specific target sum. */
int countPartitions(int n, int diff, vector<int>& arr) {
int totSum = 0;
// Calculate the total sum of elements in the array.
for (int i = 0; i < n; i++) {
totSum += arr[i];
}
/* If the total sum minus the difference is negative
or odd, it's not possible to partition the array
into subsets with the given difference.*/
if (totSum - diff < 0 || (totSum - diff) % 2) return 0;
// Calculate the target sum for one subset.
return findWays(arr, (totSum - diff) / 2);
}
};
int main() {
vector<int> arr = {5, 2, 6, 4};
int n = arr.size();
int diff = 3;
// Create an instance of the Solution class
Solution sol;
// Print the number of subsets
cout << "The number of subsets found are " << sol.countPartitions(n, diff, arr) << endl;
return 0;
}
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848586
import java.util.*;
class Solution {
// Modulus value to avoid overflow in calculations.
private static final int MOD = (int) 1e9 + 7;
/* Function to calculate the number of subsets
with a specific target sum. Uses space optimization
to store only the previous state in the DP table. */
private int findWays(int[] num, int tar) {
int n = num.length;
/* DP table to store number of ways
to achieve a certain target sum. */
int[] prev = new int[tar + 1];
/* 2 cases for target 0 when the first
element is 0: either pick it or not. */
if (num[0] == 0) prev[0] = 2;
/* 1 case for target 0 when the first
element is non-zero: just don't pick it. */
else prev[0] = 1;
/* Initialize the base case for the
first element and non-zero target. */
if (num[0] != 0 && num[0] <= tar) prev[num[0]] = 1;
/* Iterate through all elements of the
array starting from the second element. */
for (int ind = 1; ind < n; ind++) {
int[] cur = new int[tar + 1];
for (int target = 0; target <= tar; target++) {
/* Number of ways to achieve the target
sum without including the current element. */
int notTaken = prev[target];
/* Number of ways to achieve the target sum
by including the current element. */
int taken = 0;
if (num[ind] <= target)
taken = prev[target - num[ind]];
/* Total ways to achieve the target sum either
including or excluding the current element. */
cur[target] = (notTaken + taken) % MOD;
}
/* Update the previous state to the current
state for the next iteration. */
prev = cur;
}
// Return the number of subsets
return prev[tar];
}
/* Function to count the number of subsets with a
given difference. Uses the helper function findWays
to find number of subsets with a specific target sum. */
public int countPartitions(int n, int diff, int[] arr) {
int totSum = 0;
// Calculate the total sum of elements in the array.
for (int i = 0; i < n; i++) {
totSum += arr[i];
}
/* If the total sum minus the difference is negative
or odd, it's not possible to partition the array
into subsets with the given difference. */
if (totSum - diff < 0 || (totSum - diff) % 2 != 0) return 0;
// Calculate the target sum for one subset.
return findWays(arr, (totSum - diff) / 2);
}
public static void main(String[] args) {
int[] arr = {5, 2, 6, 4};
int n = arr.length;
int diff = 3;
// Create an instance of the Solution class
Solution sol = new Solution();
// Print the number of subsets
System.out.println("The number of subsets found are " + sol.countPartitions(n, diff, arr));
}
}
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374
class Solution:
# Modulus value to avoid overflow in calculations.
mod = int(1e9 + 7)
"""Function to calculate the number of subsets
with a specific target sum. Uses space optimization
to store only the previous state in the DP table."""
def findWays(self, num, tar):
n = len(num)
""" DP table to store number of ways
to achieve a certain target sum."""
prev = [0] * (tar + 1)
""" 2 cases for target 0 when the first
element is 0: either pick it or not."""
if num[0] == 0:
prev[0] = 2
else:
prev[0] = 1
""" Initialize the base case for the
first element and non-zero target."""
if num[0] != 0 and num[0] <= tar:
prev[num[0]] = 1
""" Iterate through all elements of the
array starting from the second element."""
for ind in range(1, n):
cur = [0] * (tar + 1)
for target in range(tar + 1):
""" Number of ways to achieve the target
sum without including the current element."""
not_taken = prev[target]
""" Number of ways to achieve the target sum
by including the current element."""
taken = 0
if num[ind] <= target:
taken = prev[target - num[ind]]
""" Total ways to achieve the target sum either
including or excluding the current element."""
cur[target] = (not_taken + taken) % Solution.mod
""" Update the previous state to the
current state for the next iteration."""
prev = cur
# Return the number of subsets
return prev[tar]
def countPartitions(self, n, diff, arr):
tot_sum = sum(arr)
# Checking for edge cases
if tot_sum - diff < 0 or (tot_sum - diff) % 2:
return 0
# Calculate the target sum for one subset.
return self.findWays(arr, (tot_sum - diff) // 2)
if __name__ == "__main__":
arr = [5, 2, 6, 4]
n = len(arr)
diff = 3
# Create an instance of the Solution class
sol = Solution()
# Print the number of subsets
print("The number of subsets found are", sol.countPartitions(n, diff, arr))
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576
class Solution {
// Modulus value to avoid overflow in calculations.
constructor() {
this.mod = 1e9 + 7;
}
/* Function to calculate the number of subsets
with a specific target sum. Uses space optimization
to store only the previous state in the DP table. */
findWays(num, tar) {
const n = num.length;
/* DP table to store number of ways
to achieve a certain target sum.*/
let prev = new Array(tar + 1).fill(0);
/* 2 cases for target 0 when the first
element is 0: either pick it or not.*/
if (num[0] === 0) prev[0] = 2;
else prev[0] = 1;
/* Initialize the base case for
the first element and non-zero target.*/
if (num[0] !== 0 && num[0] <= tar) prev[num[0]] = 1;
/* Iterate through all elements of the
array starting from the second element.*/
for (let ind = 1; ind < n; ind++) {
let cur = new Array(tar + 1).fill(0);
for (let target = 0; target <= tar; target++) {
/* Number of ways to achieve the target
sum without including the current element.*/
let notTaken = prev[target];
/* Number of ways to achieve the target
sum by including the current element.*/
let taken = 0;
if (num[ind] <= target)
taken = prev[target - num[ind]];
/* Total ways to achieve the target sum either
including or excluding the current element.*/
cur[target] = (notTaken + taken) % this.mod;
}
/* Update the previous state to the
current state for the next iteration.*/
prev = cur;
}
// Return the number of subsets
return prev[tar];
}
/* Function to count the number of subsets with a
given difference. Uses the helper function findWays
to find number of subsets with a specific target sum. */
countPartitions(n, diff, arr) {
const totSum = arr.reduce((sum, num) => sum + num, 0);
// Checking for edge cases
if (totSum - diff < 0 || (totSum - diff) % 2 !== 0) return 0;
// Calculate the target sum for one subset.
return this.findWays(arr, (totSum - diff) / 2);
}
}
const arr = [5, 2, 6, 4];
const n = arr.length;
const diff = 3;
// Create an instance of the Solution class
const sol = new Solution();
// Print the number of subsets
console.log("The number of subsets found are", sol.countPartitions(n, diff, arr));
Complexity Analysis:
Time Complexity: O(N*K), As, here are three nested loops that account for O(N*K) complexity.Space Complexity:O(K), As we are using an external array of size ‘K+1’ to store only one row.
Frequently Occurring Doubts
Q: Why do we check S + diff for evenness?
A: A subset sum S1 must be integer-valued. If S + diff is odd, no valid integer S1 exists.
Q: Can we solve this problem using bit manipulation?
A: Yes! We can use a bitset DP, shifting bits left by arr[i] to track possible sums efficiently.
Interview Followup Questions
Q: How would you modify this problem to return the actual subsets instead of just counting them?
A: Maintain a backtracking path (dp[i][j] storing contributing elements) to reconstruct subsets.
Q: How would this problem be solved using graph-based techniques?
A: The problem can be modeled as a graph, where each subset sum is a node, and edges represent adding elements.
Notes
Code
✅ Testcase
Input: {'arr': '[1, 1, 2, 3]', 'diff': '1'}
Expected:
3
3
Actual: -
Time: -
sec
Status: Waiting
Input: {'arr': '[1, 2, 3, 4]', 'diff': '2'}
Expected:
2
2
Actual: -
Time: -
sec
Status: Waiting
Input: {'arr': '[5, 2, 6, 4]', 'diff': '3'}
Expected:
1
1
Actual: -
Time: -
sec
Status: Waiting
Facts
- • This problem and its underlying concept of dynamic programming is a fundamental part of many algorithms used in machine learning and data analysis
- • For instance, these types of partitioning problems are often used in dividing datasets for testing and training purposes, in a way that a certain condition is met - be it the difference between sums of subsets, or maximizing the similarity of data within each subset
- • Additionally, it is also common in load balancing problems where tasks are distributed across different servers in a way that the workload difference between any two servers is minimum