Distinct subsequences

We have to find distinct subsequences of 's' in 't'. As there is no uniformity in data, there is no other way to find out than to try out all possible ways. To do so we will need to use recursion.

Steps to form the recursive solution:

Express the problem in terms of indexes: We are given two strings. We can represent them with the help of two indexes i and j. Initially, i=n-1 and j=m-1, where n and m are lengths of strings s and t Initially, we will call f(n-1,j-1), which means the count of all subsequences of string s[0…m-1] in string t[0…n-1]. We can generalize it as, f(i, j) gives the count of all distinct subsequences of t[form index 0 to j-1] in the string s[form index 0 to i-1].
Try out all possible choices at a given index: Now, i and j represent two characters from strings s and t respectively. We want to find distinct subsequences. There are only two options that make sense: either the characters represented by i and j match or they don’t.

(Case 1)When the characters match: If(s[i] == t[j]), let’s understand it with the following example:

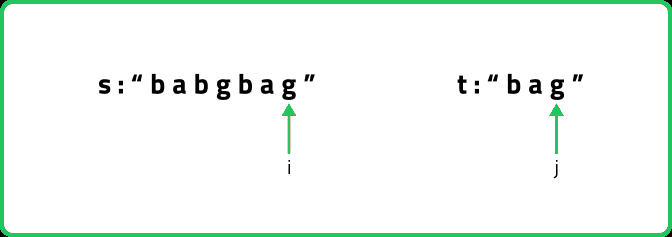
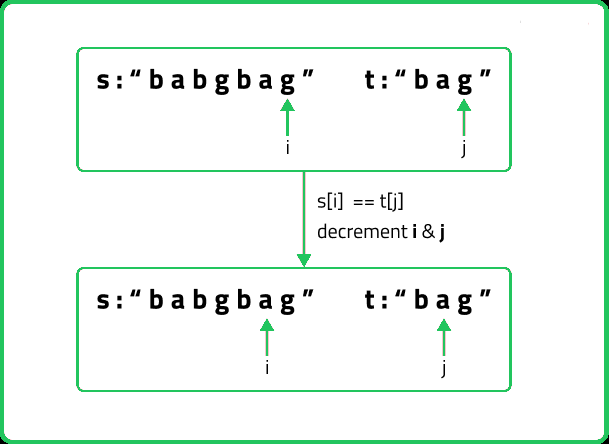
s[i] == t[j], now as the characters at i and j match, we would want to check the possibility of the remaining characters of str2 in str1 therefore we reduce the length of both the strings by 1 and call the function recursively.

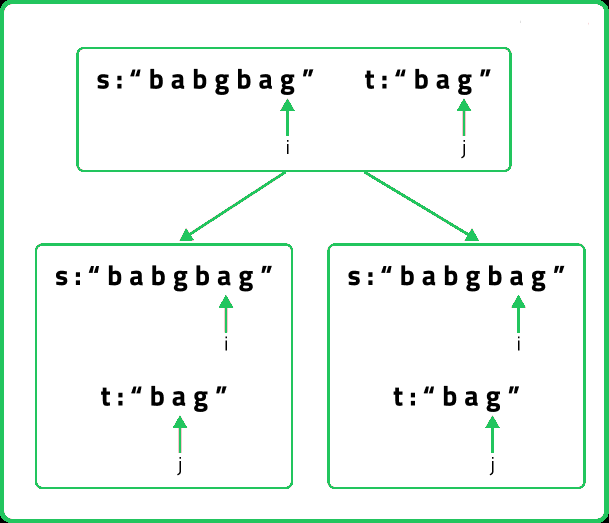
Now, if we only make the above single recursive call, we are rejecting the opportunities to find more than one subsequences because it can happen that the jth character may match with more characters in s[0…i-1], for example where there are more occurrences of ‘g’ in str1 from which also an answer needs to be explored.

To explore all such possibilities, we make another recursive call in which we reduce the length of the s string by 1 but keep the t string the same, i.e we call f(i-1,j).

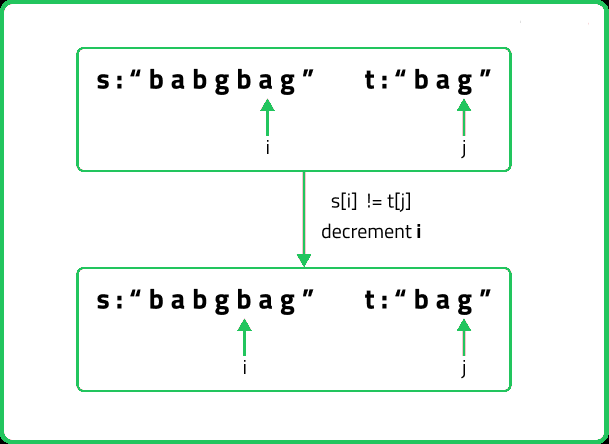
(Case 2) When the characters don’t match: If(s[i] != t[j]), it means that we don’t have any other choice than to try the next character of s and match it with the current character t.

This can be summarized as :

If(s[i] == t[j]), call f(i-1,j-1) and f(i-1,j).
If(s[i]! = t[j]), call f(i-1,j).

/*It is pseudocode and it is not related 
to any specific programming language */
f(i, j){
    if(s[i] == t[j]){
        return f(i-1, j-1) + f(i-1, j)
    }
     else
        return f(i-1, j)
}

Return the sum of choices: As we have to return the total count, we will return the sum of f(i-1,j-1) and f(i-1,j) in case 1 and simply return f(i-1,j) in case 2.
Base Cases: We are reducing i and j in our recursive relation, there can be two possibilities, either i becomes -1 or j becomes -1.

If j<0, it means we have matched all characters of s with characters of t, so we return 1.
If i<0, it means we have checked all characters of 's' but we are not able to match all characters of 't', therefore we return 0.

#include <bits/stdc++.h>
using namespace std;

class Solution{
private:	
    const int prime = 1e9 + 7;
    int countUtil(string s1, string s2, int ind1, int ind2) {
        /* If s2 has been completely matched,
        return 1 (found a valid subsequence)*/
        if (ind2 < 0)
            return 1;
    
        /* If s1 has been completely traversed
        but s2 hasn't, return 0*/
        if (ind1 < 0)
            return 0;

        int result = 0;

        /* If the characters match, consider two options:
        either leave one character in s1 and s2 or leave 
        one character in s1 and continue matching s2*/
        if (s1[ind1] == s2[ind2]) {
            int leaveOne = countUtil(s1, s2, ind1 - 1, ind2 - 1);
            int stay = countUtil(s1, s2, ind1 - 1, ind2);

            result = (leaveOne + stay) % prime;
        } else {
            /* If characters don't match, just leave
            one character in s1 and continue matching s2*/
            result = countUtil(s1, s2, ind1 - 1, ind2);
        }

        // Return the result
        return result;
    }
public:
    /* Function to count the number of
    distinct subsequences of s in t*/
	int distinctSubsequences(string s, string t){
		int lt = s.size();
		int ls = t.size();
        return countUtil(s, t, lt - 1, ls - 1);
	}
};
int main() {
    string s1 = "babgbag";
    string s2 = "bag";
    
    //Create an instace of Solution class
    Solution sol;

    // Print the result
    cout << "The Count of Distinct Subsequences is " << sol.distinctSubsequences(s1, s2);
    return 0;
}
import java.util.*;

class Solution {
    private static final int prime = (int)(1e9 + 7);
    /* Function to count the number of 
    distinct subsequences of s2 in s1*/
    private int countUtil(String s1, String s2, int ind1, int ind2) {
        /* If s2 has been completely matched,
        return 1 (found a valid subsequence)*/
        if (ind2 < 0)
            return 1;
            
        /* If s1 has been completely traversed
        but s2 hasn't, return 0*/
        if (ind1 < 0)
            return 0;

        int result = 0;

        /* If the characters match, consider two options:
        either leave one character in s1 and s2 or leave 
        one character in s1 and continue matching s2*/
        if (s1.charAt(ind1) == s2.charAt(ind2)) {
            int leaveOne = countUtil(s1, s2, ind1 - 1, ind2 - 1);
            int stay = countUtil(s1, s2, ind1 - 1, ind2);

            result = (leaveOne + stay) % prime;
        } else {
            /* If characters don't match, just leave
            one character in s1 and continue matching s2*/
            result = countUtil(s1, s2, ind1 - 1, ind2);
        }
        // Return the result
        return result;
    }
    /* Function to count the number of
    distinct subsequences of s in t*/
    public int distinctSubsequences(String s, String t) {
        int lt = s.length();
        int ls = t.length();
        return countUtil(s, t, lt - 1, ls - 1);
    }

    public static void main(String[] args) {
        String s1 = "babgbag";
        String s2 = "bag";

        //Create an instace of Solution class
        Solution sol = new Solution();
        
        // Print the result
        System.out.println("The Count of Distinct Subsequences is " + sol.distinctSubsequences(s1, s2));
    }
}
class Solution:
    prime = 10**9 + 7
    """ Function to count the number of 
    distinct subsequences of s2 in s1"""
    def countUtil(self, s1, s2, ind1, ind2):
        """ If s2 has been completely matched,
        return 1 (found a valid subsequence)"""
        if ind2 < 0:
            return 1
            
        """ If the result for this state has
        already been calculated, return it"""
        if ind1 < 0:
            return 0

        result = 0
        
        """ If the characters match, consider two options:
        either leave one character in s1 and s2 or leave 
        one character in s1 and continue matching s2"""
        if s1[ind1] == s2[ind2]:
            leaveOne = self.countUtil(s1, s2, ind1 - 1, ind2 - 1)
            stay = self.countUtil(s1, s2, ind1 - 1, ind2)

            result = (leaveOne + stay) % self.prime
        else:
            """ If characters don't match, just leave
            one character in s1 and continue matching s2"""
            result = self.countUtil(s1, s2, ind1 - 1, ind2)
        
        # Return the result
        return result
    
    """ Function to count the number of
    distinct subsequences of s in t"""
    def distinctSubsequences(self, s, t):
        lt = len(s)
        ls = len(t)
        return self.countUtil(s, t, lt - 1, ls - 1)

s1 = "babgbag"
s2 = "bag"

#Create an instace of Solution class
sol = Solution()

# Print the result
print(f"The Count of Distinct Subsequences is {sol.distinctSubsequences(s1, s2)}")
class Solution {
    constructor() {
        this.prime = 1000000007;
    }
    /* Function to count the number of
    distinct subsequences of s2 in s1*/
    countUtil(s1, s2, ind1, ind2) {
        /* If s2 has been completely matched,
        return 1 (found a valid subsequence)*/
        if (ind2 < 0) return 1;
        
        /* If s1 has been completely traversed
        but s2 hasn't, return 0*/
        if (ind1 < 0) return 0;

        let result = 0;
        
        /* If the characters match, consider two options:
        either leave one character in s1 and s2 or leave 
        one character in s1 and continue matching s2*/
        if (s1[ind1] === s2[ind2]) {
            let leaveOne = this.countUtil(s1, s2, ind1 - 1, ind2 - 1);
            let stay = this.countUtil(s1, s2, ind1 - 1, ind2);

            result = (leaveOne + stay) % this.prime;
        } else {
            /* If characters don't match, just leave
            one character in s1 and continue matching s2*/
            result = this.countUtil(s1, s2, ind1 - 1, ind2);
        }
        // Return the result
        return result;
    }
    /* Function to count the number of
    distinct subsequences of s in t*/
    distinctSubsequences(s, t) {
        let lt = s.length;
        let ls = t.length;
        return this.countUtil(s, t, lt - 1, ls - 1);
    }
}

let s1 = "babgbag";
let s2 = "bag";

//Create an instace of Solution class
let sol = new Solution();

// Print the result
console.log("The Count of Distinct Subsequences is " + sol.distinctSubsequences(s1, s2));

Complexity Analysis:

Time Complexity: Exponential

Space Complexity: O(N+M), We are using a recursion stack space (O(N+M)).

If we draw the recursion tree, we will see that there are overlapping subproblems. Hence the DP approaches can be applied to the recursive solution.

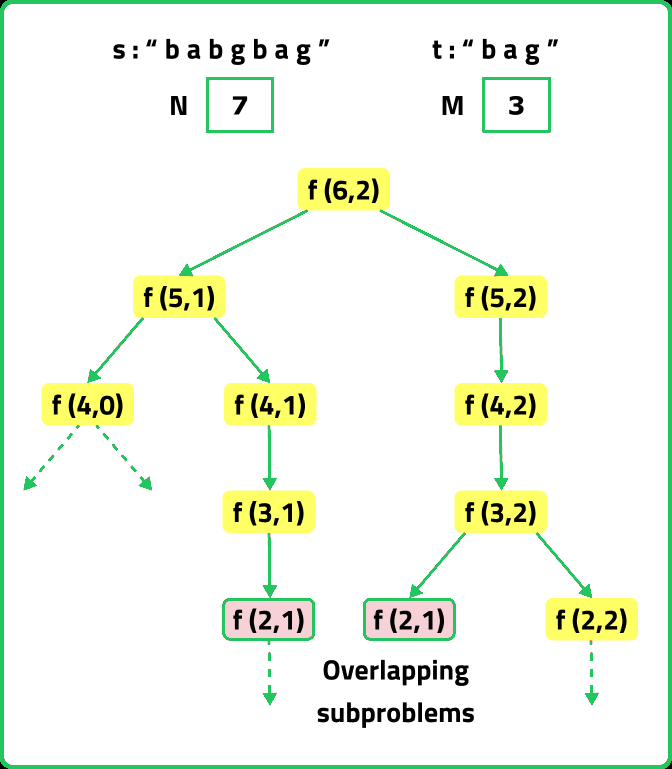
In order to convert a recursive solution to memoization the following steps will be taken:

Declare a dp array of size [n][m]: where n and m are the lengths of 's' and 't' respectively. As there are two changing parameters in the recursive solution, 'i' and 'j'. The maximum value 'i' can attain is (n-1) and 'j' can attain maximum value of (m-1). Therefore, we need 2D dp array.

The dp array shows the calculations of the subproblems, initialize it with -1 to show that no subproblem is solved yet.

While encountering an overlapping subproblem: When we come across a subproblem, for which the dp array has value other than -1, it means we have found a subproblem which has been solved before hence it is an overlapping subproblem. No need to calculate it's value again just retrieve the value from dp array and return it.
Store the value of subproblem: Whenever, a subproblem is enocountered and it is not solved yet(the value at this index will be -1 in the dp array), store the calculated value of subproblem in the array.

#include <bits/stdc++.h>
using namespace std;

class Solution{
private:	
    const int prime = 1e9 + 7;
    int countUtil(string s1, string s2, int ind1, int ind2, vector<vector<int>>& dp) {
        /* If s2 has been completely matched,
        return 1 (found a valid subsequence)*/
        if (ind2 < 0)
            return 1;
    
        /* If s1 has been completely traversed
        but s2 hasn't, return 0*/
        if (ind1 < 0)
            return 0;

        /* If the result for this state has
        already been calculated, return it*/
        if (dp[ind1][ind2] != -1)
            return dp[ind1][ind2];

        int result = 0;

        /* If the characters match, consider two options:
        either leave one character in s1 and s2 or leave 
        one character in s1 and continue matching s2*/
        if (s1[ind1] == s2[ind2]) {
            int leaveOne = countUtil(s1, s2, ind1 - 1, ind2 - 1, dp);
            int stay = countUtil(s1, s2, ind1 - 1, ind2, dp);

            result = (leaveOne + stay) % prime;
        } else {
            /* If characters don't match, just leave
            one character in s1 and continue matching s2*/
            result = countUtil(s1, s2, ind1 - 1, ind2, dp);
        }

        // Store the result and return it
        dp[ind1][ind2] = result;
        return result;
    }
public:
    /* Function to count the number of
    distinct subsequences of s in t*/
	int distinctSubsequences(string s, string t){
		int lt = s.size();
		int ls = t.size();
	    vector<vector<int>> dp(lt, vector<int>(ls, -1));
        return countUtil(s, t, lt - 1, ls - 1, dp);
	}
};
int main() {
    string s1 = "babgbag";
    string s2 = "bag";
    
    //Create an instace of Solution class
    Solution sol;

    // Print the result
    cout << "The Count of Distinct Subsequences is " << sol.distinctSubsequences(s1, s2);
    return 0;
}
import java.util.*;

class Solution {
    private static final int prime = (int)(1e9 + 7);
    /* Function to count the number of 
    distinct subsequences of s2 in s1*/
    private int countUtil(String s1, String s2, int ind1, int ind2, int[][] dp) {
        /* If s2 has been completely matched,
        return 1 (found a valid subsequence)*/
        if (ind2 < 0)
            return 1;
            
        /* If s1 has been completely traversed
        but s2 hasn't, return 0*/
        if (ind1 < 0)
            return 0;
            
        /* If the result for this state has
        already been calculated, return it*/
        if (dp[ind1][ind2] != -1)
            return dp[ind1][ind2];

        int result = 0;

        /* If the characters match, consider two options:
        either leave one character in s1 and s2 or leave 
        one character in s1 and continue matching s2*/
        if (s1.charAt(ind1) == s2.charAt(ind2)) {
            int leaveOne = countUtil(s1, s2, ind1 - 1, ind2 - 1, dp);
            int stay = countUtil(s1, s2, ind1 - 1, ind2, dp);

            result = (leaveOne + stay) % prime;
        } else {
            /* If characters don't match, just leave
            one character in s1 and continue matching s2*/
            result = countUtil(s1, s2, ind1 - 1, ind2, dp);
        }
        // Store the result and return it
        dp[ind1][ind2] = result;
        return result;
    }
    /* Function to count the number of
    distinct subsequences of s in t*/
    public int distinctSubsequences(String s, String t) {
        int lt = s.length();
        int ls = t.length();
        int[][] dp = new int[lt][ls];
        for (int[] row : dp) {
            Arrays.fill(row, -1);
        }
        return countUtil(s, t, lt - 1, ls - 1, dp);
    }

    public static void main(String[] args) {
        String s1 = "babgbag";
        String s2 = "bag";

        //Create an instace of Solution class
        Solution sol = new Solution();
        
        // Print the result
        System.out.println("The Count of Distinct Subsequences is " + sol.distinctSubsequences(s1, s2));
    }
}
class Solution:
    prime = 10**9 + 7
    """ Function to count the number of 
    distinct subsequences of s2 in s1"""
    def countUtil(self, s1, s2, ind1, ind2, dp):
        """ If s2 has been completely matched,
        return 1 (found a valid subsequence)"""
        if ind2 < 0:
            return 1
            
        """ If the result for this state has
        already been calculated, return it"""
        if ind1 < 0:
            return 0
            
        """ If the result for this state has
        already been calculated, return it"""
        if dp[ind1][ind2] != -1:
            return dp[ind1][ind2]

        result = 0
        
        """ If the characters match, consider two options:
        either leave one character in s1 and s2 or leave 
        one character in s1 and continue matching s2"""
        if s1[ind1] == s2[ind2]:
            leaveOne = self.countUtil(s1, s2, ind1 - 1, ind2 - 1, dp)
            stay = self.countUtil(s1, s2, ind1 - 1, ind2, dp)

            result = (leaveOne + stay) % self.prime
        else:
            """ If characters don't match, just leave
            one character in s1 and continue matching s2"""
            result = self.countUtil(s1, s2, ind1 - 1, ind2, dp)
        
        # Store the result and return it
        dp[ind1][ind2] = result
        return result
    
    """ Function to count the number of
    distinct subsequences of s in t"""
    def distinctSubsequences(self, s, t):
        lt = len(s)
        ls = len(t)
        dp = [[-1] * ls for _ in range(lt)]
        return self.countUtil(s, t, lt - 1, ls - 1, dp)

s1 = "babgbag"
s2 = "bag"

#Create an instace of Solution class
sol = Solution()

# Print the result
print(f"The Count of Distinct Subsequences is {sol.distinctSubsequences(s1, s2)}")
class Solution {
    constructor() {
        this.prime = 1000000007;
    }
    /* Function to count the number of
    distinct subsequences of s2 in s1*/
    countUtil(s1, s2, ind1, ind2, dp) {
        /* If s2 has been completely matched,
        return 1 (found a valid subsequence)*/
        if (ind2 < 0) return 1;
        
        /* If s1 has been completely traversed
        but s2 hasn't, return 0*/
        if (ind1 < 0) return 0;
        
        /* If the result for this state has
        already been calculated, return it*/
        if (dp[ind1][ind2] !== -1) return dp[ind1][ind2];

        let result = 0;
        
        /* If the characters match, consider two options:
        either leave one character in s1 and s2 or leave 
        one character in s1 and continue matching s2*/
        if (s1[ind1] === s2[ind2]) {
            let leaveOne = this.countUtil(s1, s2, ind1 - 1, ind2 - 1, dp);
            let stay = this.countUtil(s1, s2, ind1 - 1, ind2, dp);

            result = (leaveOne + stay) % this.prime;
        } else {
            /* If characters don't match, just leave
            one character in s1 and continue matching s2*/
            result = this.countUtil(s1, s2, ind1 - 1, ind2, dp);
        }
        // Store the result and return it
        dp[ind1][ind2] = result;
        return result;
    }
    /* Function to count the number of
    distinct subsequences of s in t*/
    distinctSubsequences(s, t) {
        let lt = s.length;
        let ls = t.length;
        let dp = Array.from({ length: lt }, () => Array(ls).fill(-1));
        return this.countUtil(s, t, lt - 1, ls - 1, dp);
    }
}

let s1 = "babgbag";
let s2 = "bag";

//Create an instace of Solution class
let sol = new Solution();

// Print the result
console.log("The Count of Distinct Subsequences is " + sol.distinctSubsequences(s1, s2));

Complexity Analysis:

Time Complexity: O(N*M), Where N is the length of string 's' and M is the length of string 't'. As there are N*M states therefore at max ‘N*M’ new problems will be solved.

Space Complexity: O(N*M) + O(N+M), We are using a recursion stack space (O(N+M)) and a 2D array ( O(N*M)).

In order to convert a recursive code to tabulation code, we try to convert the recursive code to tabulation and here are the steps:

Declare a dp array of size [n][m]: where n and m are the lengths of 's' and 't' respectively. As there are two changing parameters in the recursive solution, 'i' and 'j'. The maximum value 'i' can attain is (n-1) and 'j' can attain maximum value of (m-1). Therefore, we need 2D dp array.
Setting Base Cases in the Array: In the recursive code, our base condition was when i < 0 or j < 0, but we can’t set the dp array’s index to -1. Therefore a hack for this issue is to shift every index by 1 towards the right.

Therefore, we set the base condition (keep in mind 1-based indexing), we set the first column’s value as 1 and the first row as 1.

Iterative Computation Using Loops: Initialize two nested for loops to traverse the dp array and following the logic discussed in the recursive approach, set the value of each cell in the 2D dp array. Instead of recursive calls, use the dp array itself to find the values of intermediate calculations. Keeping in mind the shifting of indexes, as for example str1[ind1] will be converted to str1[ind1-1].
Returning the answer: At last dp[n][m] will hold the solution after the completion of whole process, as we are doing the calculations in bottom-up manner.

#include <bits/stdc++.h>
using namespace std;

class Solution{
public:	
  const int prime = 1e9 + 7;
    /* Function to count the number of
    distinct subsequences of s2 in s1*/
	int distinctSubsequences(string s, string t){
        int n = s.size();
        int m = t.size();
		vector<vector<int>> dp(n + 1, vector<int>(m + 1, 0));

        /* Initialize the first row: empty string s2
        can be matched with any non-empty s1 in one way*/
        for (int i = 0; i <= n; i++) {
            dp[i][0] = 1;
        }

        /* Initialize the first column: 
        s1 can't match any non-empty s2*/
        for (int i = 1; i <= m; i++) {
            dp[0][i] = 0;
        }

        // Fill in the DP array
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= m; j++) {
                if (s[i - 1] == t[j - 1]) {
                    /* If the characters match, consider two options:
                    either leave one character in s and t or leave 
                    one character in s and continue matching t*/
                    dp[i][j] = (dp[i - 1][j - 1] + dp[i - 1][j]) % prime;
                } else {
                    /* If the characters don't match, we can 
                    only leave the current character in s*/
                    dp[i][j] = dp[i - 1][j];
                }
            }
        }
 
        /* The value at dp[n][m] contains
        the count of distinct subsequences*/
        return dp[n][m];
	}
};
int main() {
    string s1 = "babgbag";
    string s2 = "bag";
    
    //Create an instace of Solution class
    Solution sol;

    // Print the result
    cout << "The Count of Distinct Subsequences is " << sol.distinctSubsequences(s1, s2);
    return 0;
}
import java.util.*;

class Solution {
    private static final int prime = (int)(1e9 + 7);
    /* Function to count the number of
    distinct subsequences of s in t*/
    public int distinctSubsequences(String s, String t) {
        int n = s.length();
        int m = t.length();
        
        int[][] dp = new int[n + 1][m + 1];
        
        /* Initialize the first row: empty string t can
        be matched with any non-empty s in one way*/
        for (int i = 0; i <= n; i++) {
            dp[i][0] = 1;
        }

        /* Initialize the first column:
        s can't match any non-empty t*/
        for (int i = 1; i <= m; i++) {
            dp[0][i] = 0;
        }
        
        // Fill in the DP array
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= m; j++) {
                if (s.charAt(i - 1) == t.charAt(j - 1)) {
                    /* If the characters match, consider two options:
                    either leave one character in s and t or leave 
                    one character in s and continue matching t*/
                    dp[i][j] = (dp[i - 1][j - 1] + dp[i - 1][j]) % prime;
                } else {
                    /* If the characters don't match, we can
                    only leave the current character in s*/
                    dp[i][j] = dp[i - 1][j];
                }
            }
        }
        /* The value at dp[n][m] contains
        the count of distinct subsequences*/
        return dp[n][m];
    }

    public static void main(String[] args) {
        String s1 = "babgbag";
        String s2 = "bag";

        //Create an instace of Solution class
        Solution sol = new Solution();
        
        // Print the result
        System.out.println("The Count of Distinct Subsequences is " + sol.distinctSubsequences(s1, s2));
    }
}
class Solution:
    prime = 10**9 + 7
    
    """ Function to count the number of
    distinct subsequences of s in t"""
    def distinctSubsequences(self, s, t):
        n = len(s)
        m = len(t)
        dp = [[0] * (m + 1) for _ in range(n + 1)]

        """ Initialize the first row: empty string t can 
        be matched with any non-empty s in one way"""
        for i in range(n + 1):
            dp[i][0] = 1

        """ Initialize the first column:
        s can't match any non-empty t"""
        for i in range(1, m + 1):
            dp[0][i] = 0
        
        # Fill in the DP array
        for i in range(1, n + 1):
            for j in range(1, m + 1):
                if s[i - 1] == t[j - 1]:
                    """If the characters match, consider two options:
                    either leave one character in s and t or leave
                    one character in s and continue matching t"""
                    dp[i][j] = (dp[i - 1][j - 1] + dp[i - 1][j]) % self.prime
                else:
                    """ If the characters don't match, we can 
                    only leave the current character in s"""
                    dp[i][j] = dp[i - 1][j]

        """ The value at dp[n][m] contains 
        the count of distinct subsequences"""
        return dp[n][m]

s1 = "babgbag"
s2 = "bag"

#Create an instace of Solution class
sol = Solution()

# Print the result
print(f"The Count of Distinct Subsequences is {sol.distinctSubsequences(s1, s2)}")
class Solution {
    constructor() {
        this.prime = 1000000007;
    }
    /* Function to count the number of
    distinct subsequences of s in t*/
    distinctSubsequences(s, t) {
        let n = s.length;
        let m = t.length;
        let dp = Array.from({ length: n + 1 }, () => Array(m + 1).fill(0));

        /* Initialize the first row: empty string t can 
        be matched with any non-empty s in one way*/
        for (let i = 0; i <= n; i++) {
            dp[i][0] = 1;
        }

        /* Initialize the first column:
        s can't match any non-empty t*/
        for (let i = 1; i <= m; i++) {
            dp[0][i] = 0;
        }
        // Fill in the DP array
        for (let i = 1; i <= n; i++) {
            for (let j = 1; j <= m; j++) {
                if (s[i - 1] === t[j - 1]) {
                    /* If the characters match, consider two options:
                    either leave one character in s and t or leave
                    one character in s and continue matching t*/
                    dp[i][j] = (dp[i - 1][j - 1] + dp[i - 1][j]) % this.prime;
                } else {
                    /* If the characters don't match, we can
                    only leave the current character in s*/
                    dp[i][j] = dp[i - 1][j];
                }
            }
        }

        /* The value at dp[n][m] contains 
        the count of distinct subsequences*/
        return dp[n][m];

    }
}

let s1 = "babgbag";
let s2 = "bag";

//Create an instace of Solution class
let sol = new Solution();

// Print the result
console.log("The Count of Distinct Subsequences is " + sol.distinctSubsequences(s1, s2));

Complexity Analysis:

Time Complexity: O(N*M), Where N is the length of string 's' and M is the length of string 't'. As there are two nested loops used.

Space Complexity: O(N*M), We are using a 2D array ( O(N*M)).

If we observe the relation obtained in the tabulation approach, dp[i][j] = dp[i-1][j-1] + dp[i-1][j] or dp[i][j] = dp[i-1][j]. We see that to calculate a value of a cell of the dp array, we need only the previous row values (say prev). So, we don’t need to store an entire array. Hence we can space optimize it. We will be space-optimizing this solution using only one row.

Understanding:

If we see the values required, dp[i-1][j-1] and dp[i-1][j], we can say that if we are at a column j, we will only require the values shown in the grey box from the previous row and other values will be from the cur row itself. So we do not need to store an entire array for it.

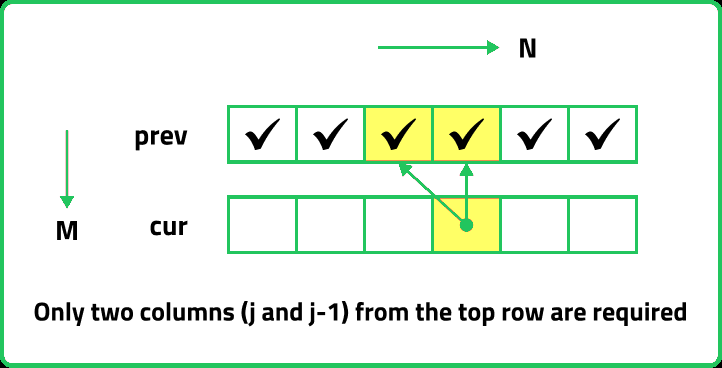
If we need only two values from the prev row, there is no need to store an entire row. We can work a bit smarter.

We can use the cur row itself to store the required value in the following way:

We take a single row ‘prev’ and initialize it to the base condition as prev[0] = 1.
Whenever we want to compute a value of the cell prev[j], we take the already existing value (prev[j] before
new computation) and prev[j-1] (if required, in case of character match).
We perform the above step on all the indexes as discussed in recursive approach.

#include <bits/stdc++.h>
using namespace std;

class Solution{
public:	
  const int prime = 1e9 + 7;
    /* Function to count the number of
    distinct subsequences of s2 in s1*/
	int distinctSubsequences(string s, string t){
        int n = s.size();
        int m = t.size();
		/* Declare an array to store the count of 
		distinct subsequences for each character in t*/
        vector<int> prev(m + 1, 0);

        // Initialize the count for an empty string 
        prev[0] = 1;

        // Iterate through s and t to calculate counts
        for (int i = 1; i <= n; i++) {
            
            /* Iterate in reverse direction to
            avoid overwriting values prematurely*/
            for (int j = m; j >= 1; j--) { 
                if (s[i - 1] == t[j - 1]) {
                    /* If the characters match, consider two options:
                    either leave one character in s and t or leave 
                    one character in s and continue matching t*/
                    prev[j] = (prev[j - 1] + prev[j]) % prime;
                }
                /* No need for an else statement since we
                can simply leave the previous count as is*/
            }
        }

        /* The value at prev[m] contains
        the count of distinct subsequences*/
        return prev[m];
	}
};
int main() {
    string s1 = "babgbag";
    string s2 = "bag";
    
    //Create an instace of Solution class
    Solution sol;

    // Print the result
    cout << "The Count of Distinct Subsequences is " << sol.distinctSubsequences(s1, s2);
    return 0;
}
import java.util.Arrays;

class Solution {
    private static final int prime = 1000000007;

    /* Function to count the number of
    distinct subsequences of s in t*/
    public int distinctSubsequences(String s, String t) {
        int n = s.length();
        int m = t.length();
        /* Declare an array to store the count of 
        distinct subsequences for each character in t*/
        int[] prev = new int[m + 1];

        // Initialize the count for an empty string 
        prev[0] = 1;

        // Iterate through s and t to calculate counts
        for (int i = 1; i <= n; i++) {
            /* Iterate in reverse direction to
            avoid overwriting values prematurely*/
            for (int j = m; j >= 1; j--) {
                if (s.charAt(i - 1) == t.charAt(j - 1)) {
                    /* If the characters match, consider two options:
                    either leave one character in s and t or leave 
                    one character in s and continue matching t*/
                    prev[j] = (prev[j - 1] + prev[j]) % prime;
                }
                /* No need for an else statement since we
                can simply leave the previous count as is*/
            }
        }

        /* The value at prev[m] contains
        the count of distinct subsequences*/
        return prev[m];
    }

    public static void main(String[] args) {
        String s1 = "babgbag";
        String s2 = "bag";

        // Create an instance of Solution class
        Solution sol = new Solution();

        // Print the result
        System.out.println("The Count of Distinct Subsequences is " + sol.distinctSubsequences(s1, s2));
    }
}
class Solution:
    prime = 10**9 + 7

    """ Function to count the number of
    distinct subsequences of s in t"""
    def distinctSubsequences(self, s, t):
        n = len(s)
        m = len(t)
        """ Declare an array to store the count of 
        distinct subsequences for each character in s"""
        prev = [0] * (m + 1)

        # Initialize the count for an empty string (base case)
        prev[0] = 1

        # Iterate through s and t to calculate counts
        for i in range(1, n + 1):
            
            """ Iterate in reverse direction to
            avoid overwriting values prematurely"""
            for j in range(m, 0, -1):
                if s[i - 1] == t[j - 1]:
                    """ If the characters match, consider two options:
                    either leave one character in s and t or leave 
                    one character in s and continue matching t"""
                    prev[j] = (prev[j - 1] + prev[j]) % self.prime
                """ No need for an else statement since we
                can simply leave the previous count as is"""

        """ The value at prev[m] contains
        the count of distinct subsequences"""
        return prev[m]

s1 = "babgbag"
s2 = "bag"

#Create an instance of Solution class
sol = Solution()

#Print the result
print(f"The Count of Distinct Subsequences is {sol.distinctSubsequences(s1, s2)}")
class Solution {
    constructor() {
        this.prime = 1000000007;
    }

    /* Function to count the number of
    distinct subsequences of s in t*/
    distinctSubsequences(s, t) {
        let n = s.length;
        let m = t.length;
        /* Declare an array to store the count of 
        distinct subsequences for each character in t*/
        let prev = Array(m + 1).fill(0);

        // Initialize the count for an empty string (base case)
        prev[0] = 1;

        // Iterate through s and t to calculate counts
        for (let i = 1; i <= n; i++) {
            /* Iterate in reverse direction to
            avoid overwriting values prematurely*/
            for (let j = m; j >= 1; j--) {
                if (s[i - 1] === t[j - 1]) {
                    /* If the characters match, consider two options:
                    either leave one character in s and t or leave 
                    one character in s and continue matching t*/
                    prev[j] = (prev[j - 1] + prev[j]) % this.prime;
                }
                /* No need for an else statement since we
                can simply leave the previous count as is*/
            }
        }

        /* The value at prev[m] contains
        the count of distinct subsequences*/
        return prev[m];
    }
}
let s1 = "babgbag";
let s2 = "bag";

//Create an instance of Solution class
let sol = new Solution();

//Print the result
console.log("The Count of Distinct Subsequences is " + sol.distinctSubsequences(s1, s2));

Complexity Analysis:

Time Complexity: O(N*M), Where N is the length of string 's' and M is the length of string 't'. As there are two nested loops used.

Space Complexity: O(M), We are using an external array of size ‘M+1’ to store only one row.

Problem List

Examples:

Constraints

Hints

Company Tags

Editorial

Steps to form the recursive solution:

Complexity Analysis:

Complexity Analysis:

Complexity Analysis:

Understanding:

Complexity Analysis:

Frequently Occurring Doubts

Interview Followup Questions

Notes

Code

Facts