Rod cutting problem

Understanding:

In oeder to solve the problem, we can build the intuition in a bit different way. Instead of cutting the rod into pieces, try to think that we need to make a rod of length 'N'(as given in the problem). Then the question becomes quite similar to unbounded knapsack problem that we did earlier, where we were doing similar work of filling up the knapsack of certain weight 'W'.

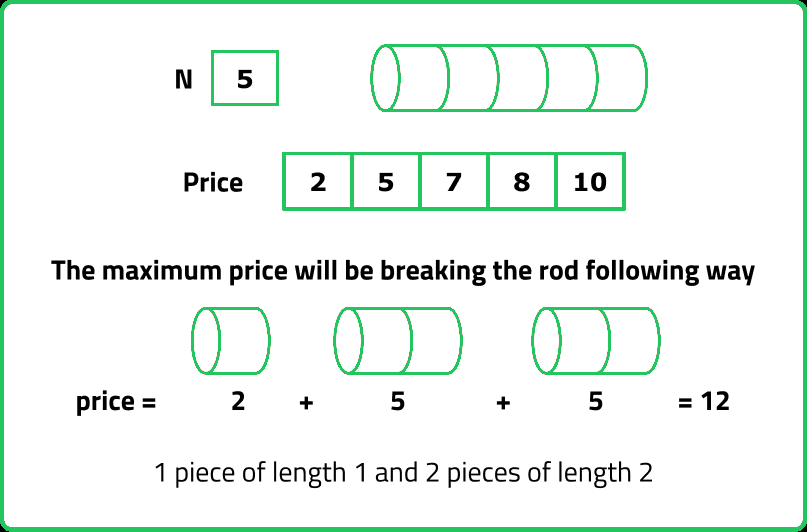
Try to pick various length in all possible ways and sum them up to make a rod of length 'N'. As we need to think of all possible ways, recursion can be used to solve this problem.

Steps to form the recursive solution:

Express the problem in terms of indexes: We are given ‘n’ items, where n is the size of the array. Their price is represented by the ‘price’ array. So clearly one parameter will be ‘ind’, i.e index upto which the array items are being considered. There is one more parameter 'N'. It keeps track of the total length of the rod that needs to be cut into parts.

So initially, we need to find f(n-1, N) where N is the total length of the rod given to us. f(n-1, N) will give the maximum value that can be acquired by cutting the rod with values from index 0 to n-1 and length of the rod N.

Try out all possible choices at a given index: As all the length needs to be explored, we will use the pick/non-pick technique.There will be two choices in each function call:

Do not include the current element in the subset: First try to find a length without considering the current index element. For this, make a recursive call to f(ind-1,target).

Include the current element in the subset: Now try to make the rod by considering the current index element as part of rod. As the current element(arr[ind]) is included, the remaining target length will be target - arr[ind]. Therefore, make a function call of f(ind,target-arr[ind]). As there are infinite supply of rods, we can stand at the same index after picking the element at an index.

Note: Consider the current element in the length of the rod only when the current length is less or equal to the 'N'.

/*It is pseudocode  and it is not tied to 
any specific programming  language*/

f(ind, N){
    not pick = 0+f(ind-1, N)
    pick = INT_MIN
    rod length = ind+1
    if( rod length <= N){
        pick = price[ind] + f(ind, N - rod length)
    }
           
}

Return max(pick and not pick): As we are looking for maximum price that we can get, so take maximum of both the choices.

/*It is pseudocode  and it is not tied to 
any specific programming  language*/

f(ind, N){
    not pick = 0+f(ind-1, N)
    pick = INT_MIN
    rod length = ind+1
    if(rod length <= N){
        pick = price[ind] + f(ind, N - rod length)
    }
    return max(pick, not pick)
}

Base cases:
If ind==0, it means for now the rod length will be 1(ind+1). In order to make a rod length of 'N' we can take the rod of length '1' for 'N' times. So the total price will be N*price[0] and we will return this for the base case.

#include <bits/stdc++.h>
using namespace std;

class Solution {
private:
    /* Function to solve the rod 
    cutting problem using recursion*/
    int func(int ind, int n, vector<int> &price) {
        /* Base case: If there is only one
        rod piece, its value is price[0] * n */
        if (ind == 0) {
            return price[0] * n;
        }

        /* Calculate the maximum value by
        not taking the current rod piece*/
        int notTaken = func(ind - 1, n, price);

        /* Calculate the length of the rod
        corresponding to the current index*/
        int rodLength = ind + 1;

        /* Initialize the value for taking
        the current rod piece as very small*/
        int taken = INT_MIN;
        
        /* If the rod length is less than or equal to
        the remaining length, consider taking it*/
        if (rodLength <= n) {
            taken = price[ind] + func(ind, n - rodLength, price);
        }

        // Return the maximum value
        return max(notTaken, taken);
    }

public:
    /* Function to initialize the DP table
    and start the rod cutting process*/
    int rodCutting(vector<int>& price, int n) {

        /* Call the utility function 
        to calculate the maximum value*/
        return func(n - 1, n, price);
    }
};

int main() {
    vector<int> price = {2, 4, 6, 8};
    int n = price.size(); 

    // Create an instance of Solution class
    Solution sol;

    // Print the result
    cout << "The Maximum value is " << sol.rodCutting(price, n) << endl;

    return 0;
}
import java.util.*;

class Solution {
    /* Function to solve the rod 
    cutting problem using recursion*/
    private int func(int ind, int n, int[] price) {
        /* Base case: If there is only one
        rod piece, its value is price[0] * n*/
        if (ind == 0) {
            return price[0] * n;
        }

        /* Calculate the maximum value by
        not taking the current rod piece*/
        int notTaken = func(ind - 1, n, price);

        /* Calculate the length of the rod
        corresponding to the current index*/
        int rodLength = ind + 1;

        /* Initialize the value for taking 
        the current rod piece as very small*/
        int taken = Integer.MIN_VALUE;
        
        /* If the rod length is less than or equal
        to the remaining length, consider taking it*/
        if (rodLength <= n) {
            taken = price[ind] + func(ind, n - rodLength, price);
        }

        // Return the maximum value 
        return Math.max(notTaken, taken);
    }

    /* Function to initialize the DP table
    and start the rod cutting process*/
    public int rodCutting(int[] price, int n) {

        /* Call the utility function 
        to calculate the maximum value*/
        return func(n - 1, n, price);
    }
}

public class Main {
    public static void main(String[] args) {
        int[] price = {2, 4, 6, 8};
        int n = price.length;

        // Create an instance of Solution class
        Solution sol = new Solution();

        // Print the result
        System.out.println("The Maximum value is " + sol.rodCutting(price, n));
    }
}
class Solution:
    """ Function to solve the rod 
    cutting problem using memoization"""
    def func(self, ind, n, price):
        """ Base case: If there is only one rod 
        piece, its value is price[0] * n"""
        if ind == 0:
            return price[0] * n

        """ Calculate the maximum value by
        not taking the current rod piece"""
        not_taken = self.func(ind - 1, n, price)

        """ Calculate the length of the rod 
        corresponding to the current index"""
        rod_length = ind + 1

        """ Initialize the value for taking the
        current rod piece as very small"""
        taken = float('-inf')
        
        """ If the rod length is less than or equal 
        to the remaining length, consider taking it"""
        if rod_length <= n:
            taken = price[ind] + self.func(ind, n - rod_length, price)

        # Return the maximum value 
        return max(not_taken, taken)

    """ Function to initialize the DP table
    and start the rod cutting process"""
    def rod_cutting(self, price, n):

        """ Call the utility function to
        calculate the maximum value"""
        return self.func(n - 1, n, price)

if __name__ == "__main__":
    # Example price array
    price = [2, 4, 6, 8]
    n = len(price)

    # Create an instance of Solution class
    sol = Solution()

    # Print the result
    print("The Maximum value is", sol.rod_cutting(price, n))
class Solution {
    /* Function to solve the rod 
    cutting problem using memoization*/
    func(ind, n, price) {
        /* Base case: If there is only one rod
        piece, its value is price[0] * n*/
        if (ind === 0) {
            return price[0] * n;
        }

        /* Calculate the maximum value by
        not taking the current rod piece*/
        const notTaken = this.func(ind - 1, n, price);

        /* Calculate the length of the rod
        corresponding to the current index*/
        const rodLength = ind + 1;

        /* Initialize the value for taking 
        the current rod piece as very small*/
        let taken = Number.NEGATIVE_INFINITY;
        
        /* If the rod length is less than or equal
        to the remaining length, consider taking it*/
        if (rodLength <= n) {
            taken = price[ind] + this.func(ind, n - rodLength, price);
        }

        // Return the maximum value 
        return Math.max(notTaken, taken);
    }

    /* Function to initialize the DP table
    and start the rod cutting process*/
    rodCutting(price, n) {

        /* Call the utility function to
        calculate the maximum value*/
        return this.func(n - 1, n, price);
    }
}

const price = [2, 4, 6, 8];
const n = price.length;

// Create an instance of Solution class
const sol = new Solution();

// Print the result
console.log("The Maximum value is", sol.rodCutting(price, n));

Time Complexity: O(2^(N)), where N is the length of the array. As, for each index, ther are two possible options.

Space Complexity:O(N), at maximum the depth of the recursive stack can go upto N.

If we draw the recursion tree, we will see that there are overlapping subproblems. Hence the DP approaches can be applied to the recursive solution.

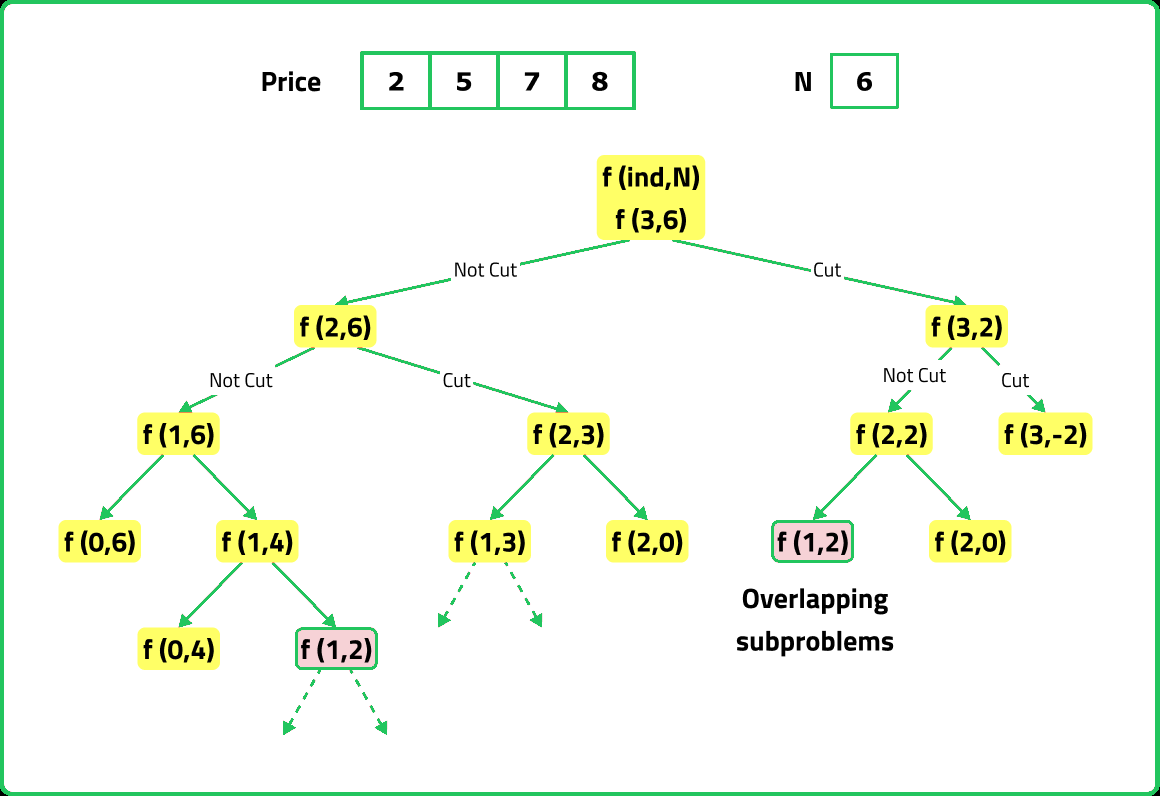
In order to convert a recursive solution to memoization the following steps will be taken:

Declare a dp array of size [n][N+1]: As there are two changing parameters in the recursive solution, 'ind' and 'W'. The maximum value 'ind' can attain is (n), where n is the size of array and for 'N', which denotes length of the rod, only values between 0 to N are possible. Therefore, we need 2D dp array.

The dp array stores the calculations of subproblems. Initialize dp array with -1, to indicate that no subproblem has been solved yet.

While encountering an overlapping subproblem: When we come across a subproblem, for which the dp array has value other than -1, it means we have found a subproblem which has been solved before hence it is an overlapping subproblem. No need to calculate it's value again just retrieve the value from dp array and return it.
Store the value of subproblem: Whenever, a subproblem is enocountered and it is not solved yet(the value at this index will be -1 in the dp array), store the calculated value of subproblem in the array.

#include <bits/stdc++.h>
using namespace std;

class Solution {
private:
    /* Function to solve the rod 
    cutting problem using memoization*/
    int func(int ind, int n, vector<int> &price, vector<vector<int>>& dp) {
        /*Base case: If there is only one
       rod piece, its value is price[0] * n*/
        if (ind == 0) {
            return price[0] * n;
        }

        /* If the result for this state is
        already calculated, return it*/
        if (dp[ind][n] != -1) {
            return dp[ind][n];
        }

        /* Calculate the maximum value by
        not taking the current rod piece*/
        int notTaken = func(ind - 1, n, price, dp);

        /* Calculate the length of the rod
        corresponding to the current index*/
        int rodLength = ind + 1;

        /* Initialize the value for taking
        the current rod piece as very small*/
        int taken = INT_MIN;
        
        /* If the rod length is less than or equal to
        the remaining length, consider taking it*/
        if (rodLength <= n) {
            taken = price[ind] + func(ind, n - rodLength, price, dp);
        }

        /* Store the maximum value in
        the DP table and return it*/
        return dp[ind][n] = max(notTaken, taken);
    }

public:
    /* Function to initialize the DP table
    and start the rod cutting process*/
    int rodCutting(vector<int>& price, int n) {
        /* Initialize DP table with 
        -1 (indicating uncalculated states)*/
        vector<vector<int>> dp(n, vector<int>(n + 1, -1));

        /* Call the utility function 
        to calculate the maximum value*/
        return func(n - 1, n, price, dp);
    }
};

int main() {
    vector<int> price = {2, 4, 6, 8};
    int n = price.size(); 

    // Create an instance of Solution class
    Solution sol;

    // Print the result
    cout << "The Maximum value is " << sol.rodCutting(price, n) << endl;

    return 0;
}
import java.util.*;

class Solution {
    /* Function to solve the rod 
    cutting problem using memoization*/
    private int func(int ind, int n, int[] price, int[][] dp) {
        /* Base case: If there is only one
        rod piece, its value is price[0] * n*/
        if (ind == 0) {
            return price[0] * n;
        }

        /* If the result for this state is
        already calculated, return it*/
        if (dp[ind][n] != -1) {
            return dp[ind][n];
        }

        /* Calculate the maximum value by
        not taking the current rod piece*/
        int notTaken = func(ind - 1, n, price, dp);

        /* Calculate the length of the rod
        corresponding to the current index*/
        int rodLength = ind + 1;

        /* Initialize the value for taking 
        the current rod piece as very small*/
        int taken = Integer.MIN_VALUE;
        
        /* If the rod length is less than or equal
        to the remaining length, consider taking it*/
        if (rodLength <= n) {
            taken = price[ind] + func(ind, n - rodLength, price, dp);
        }

        /* Store the maximum value in 
        the DP table and return it*/
        dp[ind][n] = Math.max(notTaken, taken);
        return dp[ind][n];
    }

    /* Function to initialize the DP table
    and start the rod cutting process*/
    public int rodCutting(int[] price, int n) {
        /* Initialize DP table with 
        -1 (indicating uncalculated states)*/
        int[][] dp = new int[n][n + 1];
        for (int[] row : dp) {
            Arrays.fill(row, -1);
        }

        /* Call the utility function 
        to calculate the maximum value*/
        return func(n - 1, n, price, dp);
    }
}

public class Main {
    public static void main(String[] args) {
        int[] price = {2, 4, 6, 8};
        int n = price.length;

        // Create an instance of Solution class
        Solution sol = new Solution();

        // Print the result
        System.out.println("The Maximum value is " + sol.rodCutting(price, n));
    }
}
class Solution:
    """ Function to solve the rod 
    cutting problem using memoization"""
    def func(self, ind, n, price, dp):
        """ Base case: If there is only one rod 
        piece, its value is price[0] * n"""
        if ind == 0:
            return price[0] * n

        """ If the result for this state is
        already calculated, return it"""
        if dp[ind][n] != -1:
            return dp[ind][n]

        """ Calculate the maximum value by
        not taking the current rod piece"""
        not_taken = self.func(ind - 1, n, price, dp)

        """ Calculate the length of the rod 
        corresponding to the current index"""
        rod_length = ind + 1

        """ Initialize the value for taking the
        current rod piece as very small"""
        taken = float('-inf')
        
        """ If the rod length is less than or equal 
        to the remaining length, consider taking it"""
        if rod_length <= n:
            taken = price[ind] + self.func(ind, n - rod_length, price, dp)

        """ Store the maximum value in 
        the DP table and return it"""
        dp[ind][n] = max(not_taken, taken)
        return dp[ind][n]

    """ Function to initialize the DP table
    and start the rod cutting process"""
    def rod_cutting(self, price, n):
        """ Initialize DP table with 
        -1 (indicating uncalculated states)"""
        dp = [[-1] * (n + 1) for _ in range(n)]

        """ Call the utility function to
        calculate the maximum value"""
        return self.func(n - 1, n, price, dp)

if __name__ == "__main__":
    # Example price array
    price = [2, 4, 6, 8]
    n = len(price)

    # Create an instance of Solution class
    sol = Solution()

    # Print the result
    print("The Maximum value is", sol.rod_cutting(price, n))
class Solution {
    /* Function to solve the rod 
    cutting problem using memoization*/
    func(ind, n, price, dp) {
        /* Base case: If there is only one rod
        piece, its value is price[0] * n*/
        if (ind === 0) {
            return price[0] * n;
        }

        /* If the result for this state is
        already calculated, return it*/
        if (dp[ind][n] !== -1) {
            return dp[ind][n];
        }

        /* Calculate the maximum value by
        not taking the current rod piece*/
        const notTaken = this.func(ind - 1, n, price, dp);

        /* Calculate the length of the rod
        corresponding to the current index*/
        const rodLength = ind + 1;

        /* Initialize the value for taking 
        the current rod piece as very small*/
        let taken = Number.NEGATIVE_INFINITY;
        
        /* If the rod length is less than or equal
        to the remaining length, consider taking it*/
        if (rodLength <= n) {
            taken = price[ind] + this.func(ind, n - rodLength, price, dp);
        }

        /* Store the maximum value in 
        the DP table and return it*/
        dp[ind][n] = Math.max(notTaken, taken);
        return dp[ind][n];
    }

    /* Function to initialize the DP table
    and start the rod cutting process*/
    rodCutting(price, n) {
        /* Initialize DP table with -1
        (indicating uncalculated states)*/
        const dp = Array.from({ length: n }, () => Array(n + 1).fill(-1));

        /* Call the utility function to
        calculate the maximum value*/
        return this.func(n - 1, n, price, dp);
    }
}

const price = [2, 4, 6, 8];
const n = price.length;

// Create an instance of Solution class
const sol = new Solution();

// Print the result
console.log("The Maximum value is", sol.rodCutting(price, n));

Complexity Analysis:

Time Complexity:O(N*Rod length), where N is the size of the array. As there are N*(rod length) states therefore at max ‘N*(rod length)’ new problems will be solved.

Space Complexity:O(N*rod length) + O(N), the stack space will be O(N) and a 2D array of size N*(rod length) is used.

In order to convert a recursive code to tabulation code, we try to convert the recursive code to tabulation and here are the steps:

Declare a dp array of size [n][N+1]: As there are two changing parameters in the recursive solution, 'ind' and 'N'. The maximum value 'ind' can attain is (n) and including 0 its n, where n is the size of array, for 'N' can have any values between 0 to 'N'. So we need a 2D dp array. Set its type as int and initialize it as 0.
Setting Base Cases in the Array: In the recursive code, our base condition was when 'ind' == 0, it means we were considering the first element. So for 'ind' == 0, assign (N * price[0]) to the dp array, as discussed in the recursive code.
Iterative Computation Using Loops: As we are done for the first row(ind = 0) in the base case, so ‘ind’ variable will move from 1 to n-1, whereas ‘N’ variable will move from 0 to 'N'(length). Initialize two nested for loops to traverse the dp array and following the logic discussed in the recursive approach, set the value of each cell in the 2D dp array. Instead of recursive calls, use the dp array itself to find the values of intermediate calculations.
Returning the answer: At last dp[n-1][N] will hold the solution after the completion of whole process, as we are doing the calculations in bottom-up manner.

#include <bits/stdc++.h>
using namespace std;

class Solution {
public:
    // Function to solve the rod cutting problem
    int rodCutting(vector<int>& price, int n) {
        // Initialize DP table with dimensions [n][n + 1]
        vector<vector<int>> dp(n, vector<int>(n + 1, 0));
        
        for(int length = 0; length <= n; length++){
            dp[0][length] = price[0]*length;
        }
        
        // Fill the DP table
        for (int ind = 1; ind < n; ++ind) { 
            for (int length = 1; length <= n; ++length) { 
                
                // Case when the piece is not taken
                int notTaken = 0+dp[ind - 1][length];
                
                // Case when the piece is taken
                int taken = INT_MIN;
                
                /* Length of the rod piece 
                corresponding to the current index*/
                int rodLength = ind + 1;
                
                // Check if the piece can be taken
                if (rodLength <= length) {
                    taken = price[ind] + dp[ind][length - rodLength];
                }
                
                /* Update dp[ind][length] with the maximum of 
                including or not including the current piece*/
                dp[ind][length] = max(notTaken, taken);
            }
        }
        
        // Return the result 
        return dp[n - 1][n];
    }
};

int main() {
    vector<int> price = {2, 4, 6, 8};
    int n = price.size();

    // Create an instance of Solution class
    Solution sol;

    // Print the result
    cout << "The Maximum value is " << sol.rodCutting(price, n) << endl;

    return 0;
}
import java.util.*;

class Solution {
    // Function to solve the rod cutting problem
    public int rodCutting(int[] price, int n) {
        // Initialize DP table with dimensions [n][n + 1]
        int[][] dp = new int[n][n + 1];
        
        for (int length = 0; length <= n; length++) {
            dp[0][length] = price[0] * length;
        }
        
        // Fill the DP table
        for (int ind = 1; ind < n; ++ind) { 
            for (int length = 1; length <= n; ++length) { 
                
                // Case when the piece is not taken
                int notTaken = dp[ind - 1][length];
                
                // Case when the piece is taken
                int taken = Integer.MIN_VALUE;
                
                /* Length of the rod piece 
                corresponding to the current index*/
                int rodLength = ind + 1;
                
                // Check if the piece can be taken
                if (rodLength <= length) {
                    taken = price[ind] + dp[ind][length - rodLength];
                }
                
                /* Update dp[ind][length] with the maximum of
                including or not including the current piece*/
                dp[ind][length] = Math.max(notTaken, taken);
            }
        }
        
        // Return the result
        return dp[n - 1][n];
    }

    public static void main(String[] args) {
        int[] price = {2, 4, 6, 8};
        int n = price.length;

        // Create an instance of Solution class
        Solution sol = new Solution();

        // Print the result
        System.out.println("The Maximum value is " + sol.rodCutting(price, n));
    }
}
class Solution:
    # Function to solve the rod cutting problem
    def rodCutting(self, price, n):
        # Initialize DP table with dimensions [n][n + 1]
        dp = [[0] * (n + 1) for _ in range(n)]
        
        for length in range(n + 1):
            dp[0][length] = price[0] * length
        
        # Fill the DP table
        for ind in range(1, n): 
            for length in range(1, n + 1): 
                
                # Case when the piece is not taken
                notTaken = dp[ind - 1][length]
                
                # Case when the piece is taken
                taken = float('-inf')
                
                """ Length of the rod piece 
                corresponding to the current index"""
                rodLength = ind + 1
                
                # Check if the piece can be taken
                if rodLength <= length:
                    taken = price[ind] + dp[ind][length - rodLength]
                
                """ Update dp[ind][length] with the maximum of
                including or not including the current piece"""
                dp[ind][length] = max(notTaken, taken)
        
        # Return the result
        return dp[n - 1][n]

if __name__ == "__main__":
    price = [2, 4, 6, 8]
    n = len(price)

    # Create an instance of Solution class
    sol = Solution()

    # Print the result
    print("The Maximum value is", sol.rodCutting(price, n))
class Solution {
    // Function to solve the rod cutting problem
    rodCutting(price, n) {
        // Initialize DP table with dimensions [n][n + 1]
        let dp = Array.from({ length: n }, () => Array(n + 1).fill(0));
        
        for (let length = 0; length <= n; length++) {
            dp[0][length] = price[0] * length;
        }
        
        // Fill the DP table
        for (let ind = 1; ind < n; ++ind) { 
            for (let length = 1; length <= n; ++length) { 
                
                // Case when the piece is not taken
                let notTaken = dp[ind - 1][length];
                
                // Case when the piece is taken
                let taken = -Infinity;
                
                /* Length of the rod piece 
                corresponding to the current index*/
                let rodLength = ind + 1;
                
                // Check if the piece can be taken
                if (rodLength <= length) {
                    taken = price[ind] + dp[ind][length - rodLength];
                }
                
                /* Update dp[ind][length] with the maximum 
                of including or not including the current piece*/
                dp[ind][length] = Math.max(notTaken, taken);
            }
        }
        
        // Return the result
        return dp[n - 1][n];
    }
}
    const price = [2, 4, 6, 8];
    const n = price.length;

    // Create an instance of Solution class
    const sol = new Solution();

    // Print the result
    console.log("The Maximum value is " + sol.rodCutting(price, n));

Complexity Analysis:

Time Complexity:O(N*(rod length), where N is the size of the array. There are two nested loops which accounts for N*(rod length).

Space Complexity:O(N*(rod length)), as a 2D array of size N*(rod length) is used.

If we observe the relation obtained in the tabulation approach, dp[ind][cap] = max(dp[ind-1][cap] ,dp[ind][cap-wt[ind]]. We find that to calculate a value of a cell of the dp array, only the previous row values (say prev) are needed. So, we don’t need to store an entire array. Hence we can space optimize it. We will be space optimizing this solution using only one row.

Understanding:

In the relation, dp[ind-1][cap] and dp[ind-1][cap - wt[ind]], if we are at a column, only the same column value from previous row is required and other values will be from the current row itself. So we do not need to store an entire array for it.

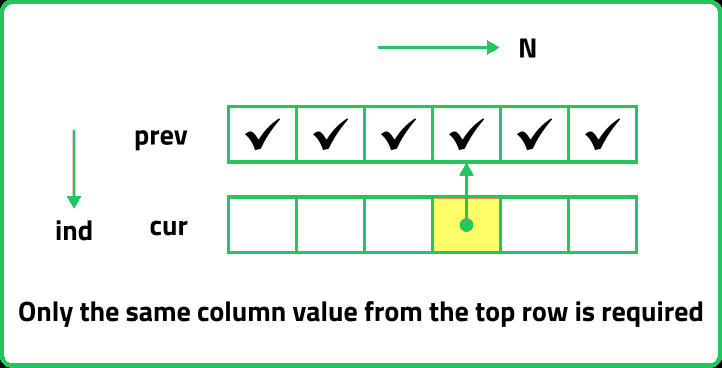
We can use the 'cur' row itself to store the required value in the following way:

Somehow make sure that the previous value( say preValue) is available to us in some manner ( we will discuss later how we got the value).
Now, let us say that we want to find the value of cell cur[3], by going through the relation we find that we need a 'preValue' and one value from the 'cur' row.
To calculate the cur[3] element, we need only a single variable (preValue). The catch is that we can initially place this preValue at the position cur[3] (before finding its updated value) and later while calculating for the current row’s cell cur[3], the value present there automatically serves as the preValue and we can use it to find the required cur[3] value.
After calculating the cur[3] value we store it at the cur[3] position so this cur[3] will automatically serve as preValue for the next row. In this way, we space-optimize the tabulation approach by just using one row.

#include <bits/stdc++.h>
using namespace std;

class Solution {
public:
    // Function to solve the rod cutting problem
    int rodCutting(vector<int>& price, int n) {
        // Initialize DP table with dimensions [n + 1]
        vector<int> prev(n+1, 0), cur(n+1, 0);
        
        for(int length = 0; length <= n; length++){
            prev[length] = price[0]*length;
        }
        
        // Fill the DP table
        for (int ind = 1; ind < n; ++ind) { 
            for (int length = 1; length <= n; ++length) { 
                
                // Case when the piece is not taken
                int notTaken = 0+prev[length];
                
                // Case when the piece is taken
                int taken = INT_MIN;
                
                /* Length of the rod piece 
                corresponding to the current index*/
                int rodLength = ind + 1;
                
                // Check if the piece can be taken
                if (rodLength <= length) {
                    taken = price[ind] + cur[length - rodLength];
                }
                
                /* Update cur[length] with the maximum of 
                including or not including the current piece*/
                cur[length] = max(notTaken, taken);
            }
            prev = cur;
        }
        
        // Return the result 
        return prev[n];
    }
};

int main() {
    vector<int> price = {2, 4, 6, 8};
    int n = price.size();

    // Create an instance of Solution class
    Solution sol;

    // Print the result
    cout << "The Maximum value is " << sol.rodCutting(price, n) << endl;

    return 0;
}
import java.util.*;

class Solution {
    // Function to solve the rod cutting problem
    public int rodCutting(int[] price, int n) {
        // Initialize DP table with dimensions [n + 1]
        int[] prev = new int[n + 1];
        int[] cur = new int[n + 1];
        
        for (int length = 0; length <= n; length++) {
            prev[length] = price[0] * length;
        }
        
        // Fill the DP table
        for (int ind = 1; ind < n; ++ind) { 
            for (int length = 1; length <= n; ++length) { 
                
                // Case when the piece is not taken
                int notTaken = prev[length];
                
                // Case when the piece is taken
                int taken = Integer.MIN_VALUE;
                
                /* Length of the rod piece 
                corresponding to the current index*/
                int rodLength = ind + 1;
                
                // Check if the piece can be taken
                if (rodLength <= length) {
                    taken = price[ind] + cur[length - rodLength];
                }
                
                /* Update cur[length] with the maximum of 
                including or not including the current piece*/
                cur[length] = Math.max(notTaken, taken);
            }
            // Copy cur to prev
            System.arraycopy(cur, 0, prev, 0, n + 1);
        }
        
        // Return the result
        return prev[n];
    }

    public static void main(String[] args) {
        int[] price = {2, 4, 6, 8};
        int n = price.length;

        // Create an instance of Solution class
        Solution sol = new Solution();

        // Print the result
        System.out.println("The Maximum value is " + sol.rodCutting(price, n));
    }
}
class Solution:
    # Function to solve the rod cutting problem
    def rodCutting(self, price, n):
        # Initialize DP table with dimensions [n + 1]
        prev = [0] * (n + 1)
        cur = [0] * (n + 1)
        
        for length in range(n + 1):
            prev[length] = price[0] * length
        
        # Fill the DP table
        for ind in range(1, n): 
            for length in range(1, n + 1): 
                
                # Case when the piece is not taken
                notTaken = prev[length]
                
                # Case when the piece is taken
                taken = float('-inf')
                
                """ Length of the rod piece 
                corresponding to the current index"""
                rodLength = ind + 1
                
                # Check if the piece can be taken
                if rodLength <= length:
                    taken = price[ind] + cur[length - rodLength]
                
                """ Update cur[length] with the maximum of 
                including or not including the current piece"""
                cur[length] = max(notTaken, taken)
            
            # Copy cur to prev
            prev = cur[:]
        
        # Return the result
        return prev[n]

if __name__ == "__main__":
    price = [2, 4, 6, 8]
    n = len(price)

    # Create an instance of Solution class
    sol = Solution()

    # Print the result
    print("The Maximum value is", sol.rodCutting(price, n))
class Solution {
    // Function to solve the rod cutting problem
    rodCutting(price, n) {
        // Initialize DP table with dimensions [n + 1]
        let prev = new Array(n + 1).fill(0);
        let cur = new Array(n + 1).fill(0);
        
        for (let length = 0; length <= n; length++) {
            prev[length] = price[0] * length;
        }
        
        // Fill the DP table
        for (let ind = 1; ind < n; ++ind) { 
            for (let length = 1; length <= n; ++length) { 
                
                // Case when the piece is not taken
                let notTaken = prev[length];
                
                // Case when the piece is taken
                let taken = -Infinity;
                
                /* Length of the rod piece 
                corresponding to the current index*/
                let rodLength = ind + 1;
                
                // Check if the piece can be taken
                if (rodLength <= length) {
                    taken = price[ind] + cur[length - rodLength];
                }
                
                /* Update cur[length] with the maximum of 
                including or not including the current piece*/
                cur[length] = Math.max(notTaken, taken);
            }
            // Copy cur to prev
            for (let i = 0; i <= n; i++) {
                prev[i] = cur[i];
            }
        }
        
        // Return the result
        return prev[n];
    }
}
    const price = [2, 4, 6, 8];
    const n = price.length;

    // Create an instance of Solution class
    const sol = new Solution();

    // Print the result
    console.log("The Maximum value is " + sol.rodCutting(price, n));

Complexity Analysis:

Time Complexity:O(N*(rod length), where N is the size of the array. There are two nested loops which accounts for N*(rod length).

Space Complexity:O(rod length), as arrays of size (rod length+1) are used.

Problem List

Examples:

Constraints

Hints

Company Tags

Editorial

Understanding:

Steps to form the recursive solution:

Complexity Analysis:

Complexity Analysis:

Understanding:

Complexity Analysis:

Frequently Occurring Doubts

Interview Followup Questions

Notes

Code