Sum of Subarray Minimums

Intuition:

The brute force way to solve this problem is by generating all the subarrays and finding the minimum in all of them. All the minimums can be summed up while taking modulus with 10⁹ + 7 to return the result.

Approach:

Initialize a variable to store the required sum with 0 initially.
Traverse on the array. Initialize a variable to store the minimum element in the subarray.
Use a nested loop to traverse for all the subarrays and find the minimum of each subarray. Update the sum for each subarray.
Once all the subarrays are taken into consideration, the result will be stored in the sum variable.

Dry Run:

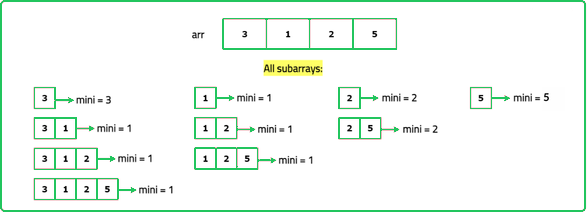
Solution:

#include <bits/stdc++.h>
using namespace std;

class Solution {
public:

   /* Function to find the sum of the 
   minimum value in each subarray */
   int sumSubarrayMins(vector<int> &arr) {
       
       // Size of array
       int n = arr.size();
       
       int mod = 1e9 + 7; // Mod value
       
       // To store the sum
       int sum = 0;
       
       // Traverse on the array
       for(int i=0; i < n; i++) {
           
           // To store the minimum of subarray
           int mini = arr[i];
           
           /* Nested loop to get all 
           subarrays starting from index i */
           for(int j=i; j < n; j++) {
               
               // Update the minimum value
               mini = min(mini, arr[j]);
               
               // Update the sum
               sum = (sum + mini) % mod;
           }
       }
       
       // Return the computed sum
       return sum;
   }
};

int main() {
   vector<int> arr = {3, 1, 2, 5};
   
   /* Creating an instance of 
   Solution class */
   Solution sol; 
   
   /* Function call to find the sum of the 
   minimum value in each subarray */
   int ans = sol.sumSubarrayMins(arr);
   
   cout << "The sum of minimum value in each subarray is: " << ans;
   
   return 0;
}
import java.util.*;

class Solution {

   /* Function to find the sum of the 
   minimum value in each subarray */
   public int sumSubarrayMins(int[] arr) {
       
       // Size of array
       int n = arr.length;
       
       int mod = (int)1e9 + 7; // Mod value
       
       // To store the sum
       int sum = 0;
       
       // Traverse on the array
       for(int i = 0; i < n; i++) {
           
           // To store the minimum of subarray
           int mini = arr[i];
           
           /* Nested loop to get all 
           subarrays starting from index i */
           for(int j = i; j < n; j++) {
               
               // Update the minimum value
               mini = Math.min(mini, arr[j]);
               
               // Update the sum
               sum = (sum + mini) % mod;
           }
       }
       
       // Return the computed sum
       return sum;
   }

   public static void main(String[] args) {
       int[] arr = {3, 1, 2, 5};
       
       /* Creating an instance of 
       Solution class */
       Solution sol = new Solution(); 
       
       /* Function call to find the sum of the 
       minimum value in each subarray */
       int ans = sol.sumSubarrayMins(arr);
       
       System.out.println("The sum of minimum value in each subarray is: " + ans);
   }
}
class Solution:
   def sumSubarrayMins(self, arr):
       
       # Size of array
       n = len(arr)
       
       mod = int(1e9 + 7)  # Mod value
       
       # To store the sum
       total_sum = 0
       
       # Traverse on the array
       for i in range(n):
           
           # To store the minimum of subarray
           mini = arr[i]
           
           # Nested loop to get all 
           # subarrays starting from index i
           for j in range(i, n):
               
               # Update the minimum value
               mini = min(mini, arr[j])
               
               # Update the sum
               total_sum = (total_sum + mini) % mod
       
       # Return the computed sum
       return total_sum

# Main function to test the solution
if __name__ == "__main__":
   arr = [3, 1, 2, 5]
   
   # Creating an instance of Solution class
   sol = Solution()
   
   # Function call to find the sum of the 
   # minimum value in each subarray
   ans = sol.sumSubarrayMins(arr)
   
   print("The sum of minimum value in each subarray is:", ans)
class Solution {

   /* Function to find the sum of the 
   minimum value in each subarray */
   sumSubarrayMins(arr) {
       
       // Size of array
       let n = arr.length;
       
       let mod = 1e9 + 7; // Mod value
       
       // To store the sum
       let sum = 0;
       
       // Traverse on the array
       for (let i = 0; i < n; i++) {
           
           // To store the minimum of subarray
           let mini = arr[i];
           
           /* Nested loop to get all 
           subarrays starting from index i */
           for (let j = i; j < n; j++) {
               
               // Update the minimum value
               mini = Math.min(mini, arr[j]);
               
               // Update the sum
               sum = (sum + mini) % mod;
           }
       }
       
       // Return the computed sum
       return sum;
   }
}

// Main function to test the solution
const arr = [3, 1, 2, 5];

/* Creating an instance of 
Solution class */
const sol = new Solution(); 

/* Function call to find the sum of the 
minimum value in each subarray */
const ans = sol.sumSubarrayMins(arr);

console.log("The sum of minimum value in each subarray is:", ans);

Complexity Analysis:

Time Complexity: O(N²)
Using two nested loops.

Space Complexity: O(1)
Using only a couple of variables.

Pre Requisites: Next Greater Element

Intuition:

Consider the following example:
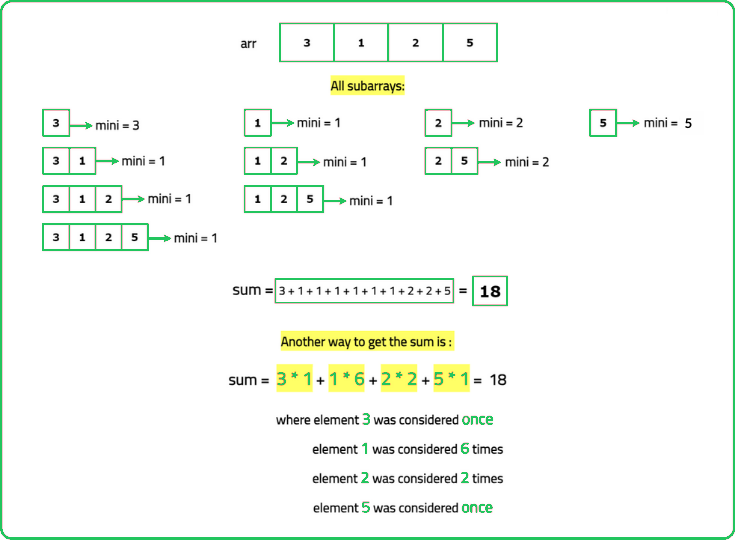
Hence it is clear that instead of generating all the subarrays and finding the minimum in each subarray to find the sum, we can get the required sum by finding the number of times(frequency) an element in the array will be considered in sum.

Considering the above dry run, we can see that:

Element 3 is contributing for a total of 3 times.
Element 1 is contributing for a total of 6 times.
Element 2 is contributing for a total of 2 times.
Element 4 is contributing for a total of 1 time..

How to find the frequency of an element in the required sum?

To find the frequency, the number of subarrays where the current element will be minimum must be known.

Understanding:

Consider the following example:

It can be seen that the current element will be considered in all those subarrays that:

Do not start with the previous smaller element (if it exists), which includes the current element.
Do not end with the next smaller element (if it exists), which includes the current element.

Finding count of required subarrays:

The count of subarrays that contain the current element as the minimum element is the subarrays whose:

Starting index lies in the range (psee[ind], ind] (excluding psee(ind) and including ind).
Count of such subarrays is: ind - (psee[ind] + 1) + 1, i.e.,
Count of such subarrays is: ind - psee[ind]. and,
Ending index lies in the range [ind, nse[ind]) (including ind and excluding nse[ind]).
Count of such subarrays is: (nse[ind] - 1) - ind + 1, i.e.,
Count of such subarrays is: nse[ind] - ind.

(where pse[ind] and nse[ind] refer to the indices of previous smallest element and the next smaller element for the element at index ind.)

Hence, the count of subarrays having the current element (having index ind) as the minimum element is:
(ind - psee[ind]) * (nse[ind] - ind).

Edge Cases:

(Yet to insert)

Approach:

For each element in the array, find the index of the next smaller element(NSE) to the right. Use a stack to efficiently track these indices.
For each element in the array, find the index of the previous smaller or equal element(PSEE) to the left. Use a stack to efficiently track these indices.
For each element in the array, calculate its contribution to the sum of subarray minimums based on its frequency as the minimum in the subarrays. Use the indices from NSE and PSEE to determine the count of subarrays where the current element is the minimum.
Multiply the frequency obtained by the element's value to get its contribution and add this to the total sum. The result is computed modulo 10⁹ + 7 to handle large numbers.

Dry Run:

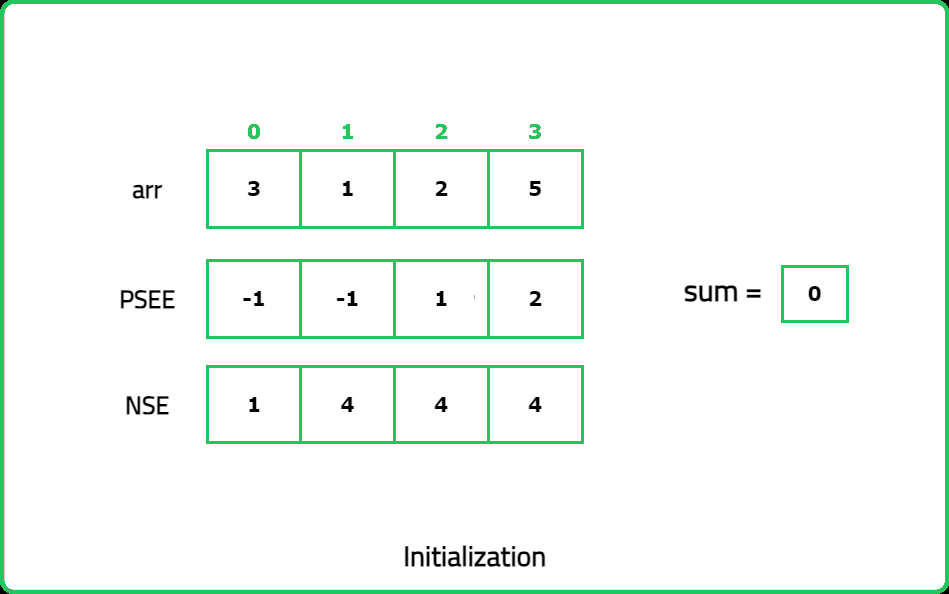
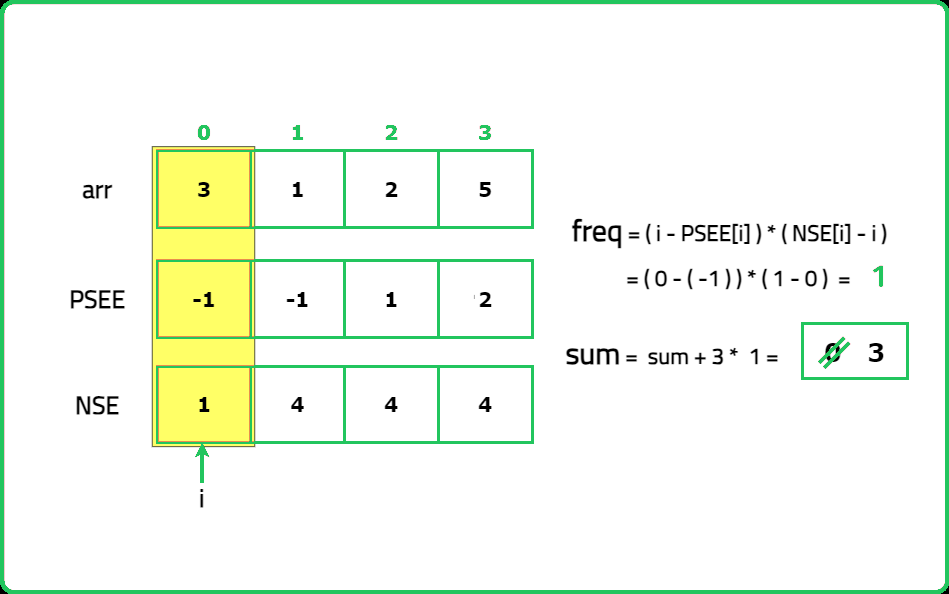
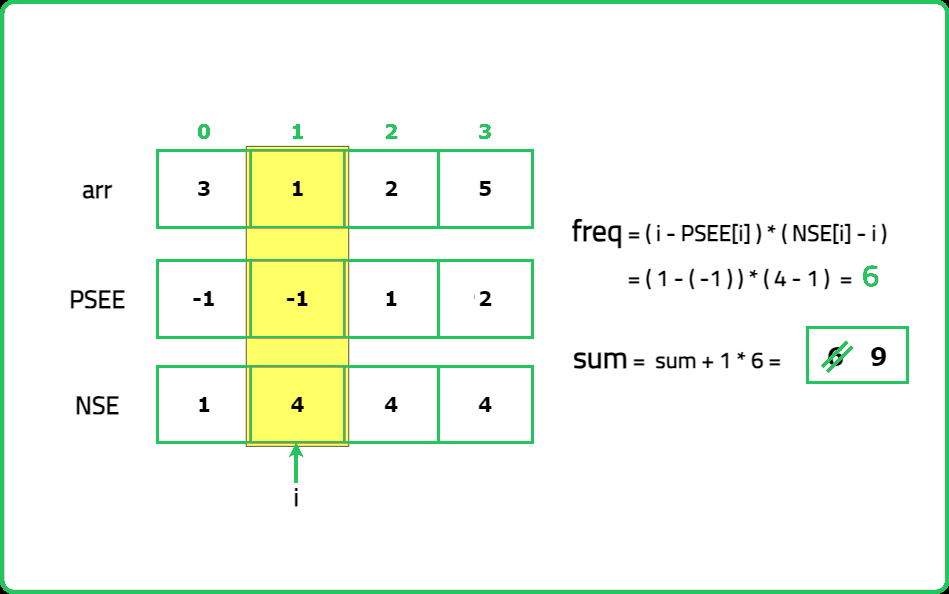
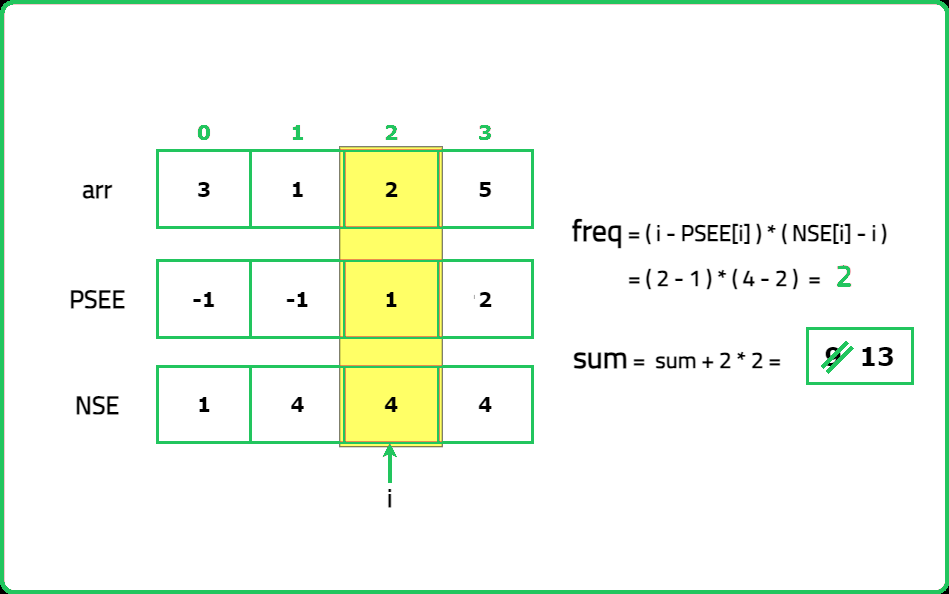
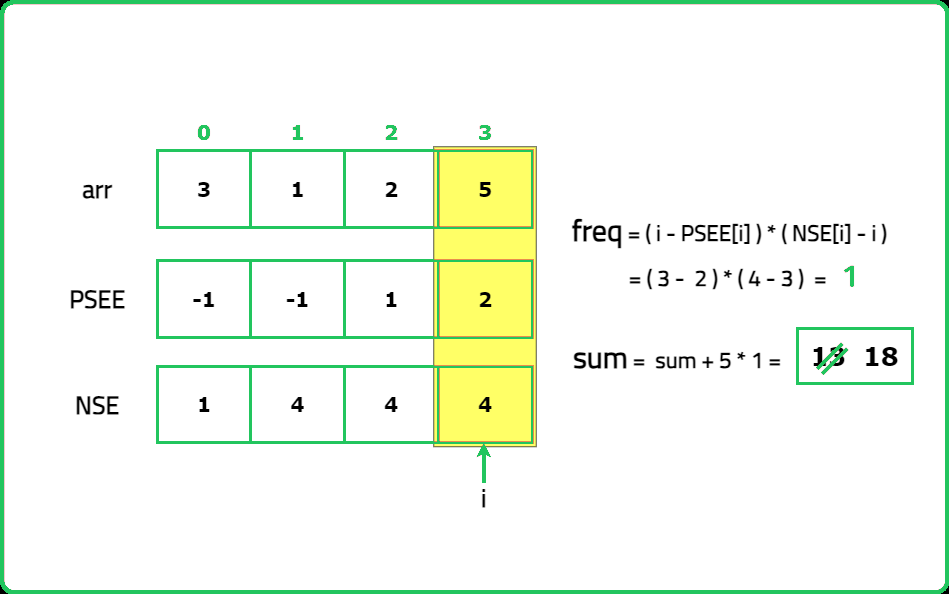
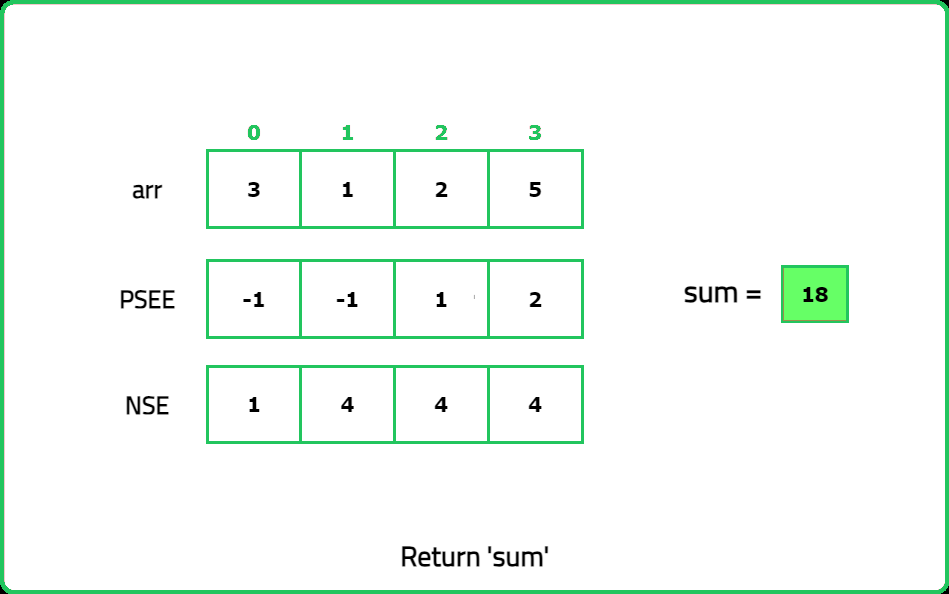
Solution:

#include <bits/stdc++.h>
using namespace std;

class Solution {
private:
    /* Function to find the indices of 
    next smaller elements */
    vector<int> findNSE(vector<int> &arr) {
        
        // Size of array
        int n = arr.size();
        
        // To store the answer
        vector<int> ans(n);
        
        // Stack 
        stack<int> st;
        
        // Start traversing from the back
        for(int i = n - 1; i >= 0; i--) {
            
            // Get the current element
            int currEle = arr[i];
            
            /* Pop the elements in the stack until 
            the stack is not empty and the top 
            element is not the smaller element */
            while(!st.empty() && arr[st.top()] >= arr[i]){
                st.pop();
            }
            
            // Update the answer
            ans[i] = !st.empty() ? st.top() : n;
            
            /* Push the index of current 
            element in the stack */
            st.push(i);
        }
        
        // Return the answer
        return ans;
    }
    
    /* Function to find the indices of 
    previous smaller or equal elements */
    vector<int> findPSEE(vector<int> &arr) {
        
        // Size of array
        int n = arr.size();
        
        // To store the answer
        vector<int> ans(n);
        
        // Stack 
        stack<int> st;
        
        // Traverse on the array
        for(int i=0; i < n; i++) {
            
            // Get the current element
            int currEle = arr[i];
            
            /* Pop the elements in the stack until 
            the stack is not empty and the top 
            elements are greater than the current element */
            while(!st.empty() && arr[st.top()] > arr[i]){
                st.pop();
            }
            
            // Update the answer
            ans[i] = !st.empty() ? st.top() : -1;
            
            /* Push the index of current 
            element in the stack */
            st.push(i);
        }
        
        // Return the answer
        return ans;
    }
    
public:

    /* Function to find the sum of the 
    minimum value in each subarray */
    int sumSubarrayMins(vector<int> &arr) {
        
        vector<int> nse = 
            findNSE(arr);
        
        vector<int> psee =
            findPSEE(arr);
        
        // Size of array
        int n = arr.size();
        
        int mod = 1e9 + 7; // Mod value
        
        // To store the sum
        int sum = 0;
        
        // Traverse on the array
        for(int i=0; i < n; i++) {
            
            // Count of first type of subarrays
            int left = i - psee[i];
            
            // Count of second type of subarrays
            int right = nse[i] - i;
            
            /* Count of subarrays where 
            current element is minimum */
            long long freq = left*right*1LL;
            
            // Contribution due to current element 
            int val = (freq*arr[i]*1LL) % mod;
            
            // Updating the sum
            sum = (sum + val) % mod;
        }
        
        // Return the computed sum
        return sum;
    }
};

int main() {
    vector<int> arr = {3, 1, 2, 5};
    
    /* Creating an instance of 
    Solution class */
    Solution sol; 
    
    /* Function call to find the sum of the 
    minimum value in each subarray */
    int ans = sol.sumSubarrayMins(arr);
    
    cout << "The sum of minimum value in each subarray is: " << ans;
    
    return 0;
}
import java.util.*;

class Solution {
    /* Function to find the indices of 
    next smaller elements */
    private int[] findNSE(int[] arr) {
        
        // Size of array
        int n = arr.length;
        
        // To store the answer
        int[] ans = new int[n];
        
        // Stack 
        Stack<Integer> st = new Stack<>();
        
        // Start traversing from the back
        for (int i = n - 1; i >= 0; i--) {
            
            // Get the current element
            int currEle = arr[i];
            
            /* Pop the elements in the stack until 
            the stack is not empty and the top 
            element is not the smaller element */
            while (!st.isEmpty() && arr[st.peek()] >= arr[i]) {
                st.pop();
            }
            
            // Update the answer
            ans[i] = !st.isEmpty() ? st.peek() : n;
            
            /* Push the index of current 
            element in the stack */
            st.push(i);
        }
        
        // Return the answer
        return ans;
    }
    
    /* Function to find the indices of 
    previous smaller or equal elements */
    private int[] findPSEE(int[] arr) {
        
        // Size of array
        int n = arr.length;
        
        // To store the answer
        int[] ans = new int[n];
        
        // Stack 
        Stack<Integer> st = new Stack<>();
        
        // Traverse on the array
        for (int i = 0; i < n; i++) {
            
            // Get the current element
            int currEle = arr[i];
            
            /* Pop the elements in the stack until 
            the stack is not empty and the top 
            elements are greater than the current element */
            while (!st.isEmpty() && arr[st.peek()] > arr[i]) {
                st.pop();
            }
            
            // Update the answer
            ans[i] = !st.isEmpty() ? st.peek() : -1;
            
            /* Push the index of current 
            element in the stack */
            st.push(i);
        }
        
        // Return the answer
        return ans;
    }

    /* Function to find the sum of the 
    minimum value in each subarray */
    public int sumSubarrayMins(int[] arr) {
        
        int[] nse = findNSE(arr);
        int[] psee = findPSEE(arr);
        
        // Size of array
        int n = arr.length;
        
        int mod = (int)1e9 + 7; // Mod value
        
        // To store the sum
        int sum = 0;
        
        // Traverse on the array
        for (int i = 0; i < n; i++) {
            
            // Count of first type of subarrays
            int left = i - psee[i];
            
            // Count of second type of subarrays
            int right = nse[i] - i;
            
            /* Count of subarrays where 
            current element is minimum */
            long freq = left * right * 1L;
            
            // Contribution due to current element 
            int val = (int)((freq * arr[i]) % mod);
            
            // Updating the sum
            sum = (sum + val) % mod;
        }
        
        // Return the computed sum
        return sum;
    }

    public static void main(String[] args) {
        int[] arr = {3, 1, 2, 5};
        
        // Creating an instance of Solution class
        Solution sol = new Solution(); 
        
        // Function call to find the sum of the minimum value in each subarray
        int ans = sol.sumSubarrayMins(arr);
        
        System.out.println("The sum of minimum value in each subarray is: " + ans);
    }
}
class Solution:
    # Function to find the indices 
    # of next smaller elements
    def findNSE(self, arr):
        
        # Size of array
        n = len(arr)
        
        # To store the answer
        ans = [0] * n
        
        # Stack 
        st = []
        
        # Start traversing from the back
        for i in range(n - 1, -1, -1):
            
            # Get the current element
            currEle = arr[i]
            
            # Pop the elements in the stack until 
            # the stack is not empty and the top 
            # element is not the smaller element
            while st and arr[st[-1]] >= arr[i]:
                st.pop()
            
            # Update the answer
            ans[i] = st[-1] if st else n
            
            # Push the index of current 
            # element in the stack
            st.append(i)
        
        # Return the answer
        return ans
    
    # Function to find the indices of 
    # previous smaller or equal elements
    def findPSEE(self, arr):
        
        # Size of array
        n = len(arr)
        
        # To store the answer
        ans = [0] * n
        
        # Stack 
        st = []
        
        # Traverse on the array
        for i in range(n):
            
            # Get the current element
            currEle = arr[i]
            
            # Pop the elements in the stack until 
            # the stack is not empty and the top 
            # elements are greater than the current element
            while st and arr[st[-1]] > arr[i]:
                st.pop()
            
            # Update the answer
            ans[i] = st[-1] if st else -1
            
            # Push the index of current 
            # element in the stack
            st.append(i)
        
        # Return the answer
        return ans

    # Function to find the sum of the 
    # minimum value in each subarray
    def sumSubarrayMins(self, arr):
        
        nse = self.findNSE(arr)
        psee = self.findPSEE(arr)
        
        # Size of array
        n = len(arr)
        
        mod = int(1e9 + 7)  # Mod value
        
        # To store the sum
        total_sum = 0
        
        # Traverse on the array
        for i in range(n):
            
            # Count of first type of subarrays
            left = i - psee[i]
            
            # Count of second type of subarrays
            right = nse[i] - i
            
            # Count of subarrays where 
            # current element is minimum
            freq = left * right * 1
            
            # Contribution due to current element 
            val = (freq * arr[i]) % mod
            
            # Updating the sum
            total_sum = (total_sum + val) % mod
        
        # Return the computed sum
        return total_sum

# Main function to test the solution
if __name__ == "__main__":
    arr = [3, 1, 2, 5]
    
    # Creating an instance of Solution class
    sol = Solution()
    
    # Function call to find the sum of the 
    # minimum value in each subarray
    ans = sol.sumSubarrayMins(arr)
    
    print("The sum of minimum value in each subarray is:", ans)
class Solution {
    /* Function to find the indices 
    of next smaller elements */
    findNSE(arr) {
        
        // Size of array
        const n = arr.length;
        
        // To store the answer
        const ans = new Array(n).fill(0);
        
        // Stack 
        const st = [];
        
        // Start traversing from the back
        for (let i = n - 1; i >= 0; i--) {
            
            // Get the current element
            const currEle = arr[i];
            
            // Pop the elements in the stack until 
            // the stack is not empty and the top 
            // element is not the smaller element
            while (st.length > 0 && arr[st[st.length - 1]] >= arr[i]) {
                st.pop();
            }
            
            // Update the answer
            ans[i] = st.length > 0 ? st[st.length - 1] : n;
            
            /* Push the index of current 
            element in the stack */
            st.push(i);
        }
        
        // Return the answer
        return ans;
    }
    
    /* Function to find the indices of 
    previous smaller or equal elements */
    findPSEE(arr) {
        
        // Size of array
        const n = arr.length;
        
        // To store the answer
        const ans = new Array(n).fill(0);
        
        // Stack 
        const st = [];
        
        // Traverse on the array
        for (let i = 0; i < n; i++) {
            
            // Get the current element
            const currEle = arr[i];
            
            // Pop the elements in the stack until 
            // the stack is not empty and the top 
            // elements are greater than the current element
            while (st.length > 0 && arr[st[st.length - 1]] > arr[i]) {
                st.pop();
            }
            
            // Update the answer
            ans[i] = st.length > 0 ? st[st.length - 1] : -1;
            
            /* Push the index of current 
            element in the stack */
            st.push(i);
        }
        
        // Return the answer
        return ans;
    }

    /* Function to find the sum of 
    the minimum value in each subarray */
    sumSubarrayMins(arr) {
        
        const nse = this.findNSE(arr);
        const psee = this.findPSEE(arr);
        
        // Size of array
        const n = arr.length;
        
        const mod = 1e9 + 7; // Mod value
        
        // To store the sum
        let sum = 0;
        
        // Traverse on the array
        for (let i = 0; i < n; i++) {
            
            // Count of first type of subarrays
            const left = i - psee[i];
            
            // Count of second type of subarrays
            const right = nse[i] - i;
            
            /* Count of subarrays where 
            current element is minimum */
            const freq = left * right * 1;
            
            // Contribution due to current element 
            const val = (freq * arr[i]) % mod;
            
            // Updating the sum
            sum = (sum + val) % mod;
        }
        
        // Return the computed sum
        return sum;
    }
}

// Main function to test the solution
const arr = [3, 1, 2, 5];

/* Creating an instance of 
Solution class */
const sol = new Solution(); 

/* Function call to find the sum of the 
minimum value in each subarray */
const ans = sol.sumSubarrayMins(arr);

console.log("The sum of minimum value in each subarray is:", ans);

Complexity Analysis:

Time Complexity: O(N) (where N is the size of given array)

Finding the indices of next smaller elements and previous smaller elements take O(2*N) time each.
Calculating the sum of subarrays minimum takes O(N) time.

Space Complexity: O(N)

Finding the indices of the next smaller elements and previous smaller elements takes O(N) space each due to stack space.
Storing the indices of the next smaller elements and previous smaller elements takes O(N) space each.

Problem List

Examples:

Constraints

Hints

Company Tags

Editorial

Intuition:

Approach:

Dry Run:

Solution:

Complexity Analysis:

Intuition:

How to find the frequency of an element in the required sum?

Understanding:

Finding count of required subarrays:

Edge Cases:

Approach:

Dry Run:

Solution:

Complexity Analysis:

Frequently Occurring Doubts

Interview Followup Questions

Notes

Code