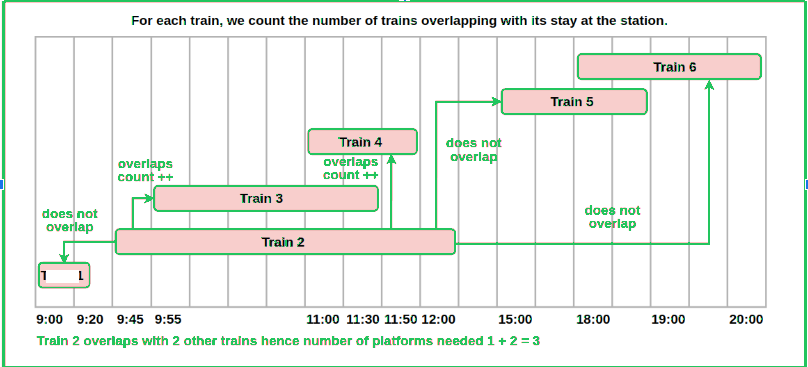
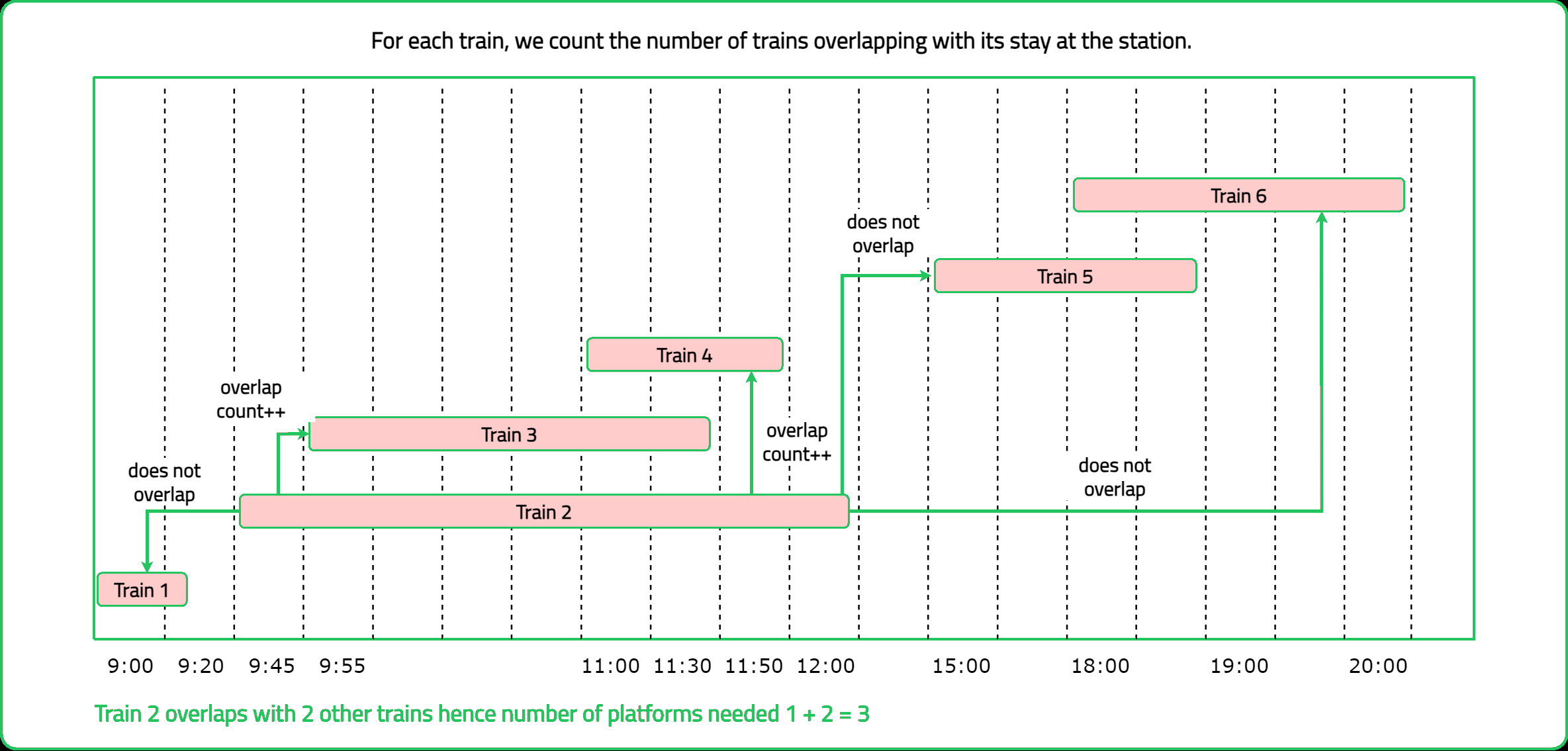
123456789101112131415161718192021222324252627282930313233343536373839404142
#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
// To find number of platforms
int findPlatform(vector<int>& Arrival, vector<int>& Departure) {
int n = Arrival.size();
// Sort both arrival and departure arrays
sort(Arrival.begin(), Arrival.end());
sort(Departure.begin(), Departure.end());
int ans = 1;
int count = 1;
int i = 1, j = 0;
// Iterate through the arrays
while (i < n && j < n) {
if (Arrival[i] <= Departure[j]) {
// Increment count
count++;
i++;
} else {
// Decrement Count
count--;
j++;
}
// Find maximum
ans = max(ans, count);
}
return ans;
}
};
int main() {
vector<int> arr = {900, 945, 955, 1100, 1500, 1800};
vector<int> dep = {920, 1200, 1130, 1150, 1900, 2000};
Solution sol;
cout << "Minimum number of Platforms required: " << sol.findPlatform(arr, dep) << endl;
}
12345678910111213141516171819202122232425262728293031323334353637383940
import java.util.*;
class Solution {
// To find number of platforms
public int findPlatform(int[] Arrival, int[] Departure) {
int n = Arrival.length;
// Sort both arrival and departure arrays
Arrays.sort(Arrival);
Arrays.sort(Departure);
int ans = 1;
int count = 1;
int i = 1, j = 0;
// Iterate through the arrays
while (i < n && j < n) {
if (Arrival[i] <= Departure[j]) {
// Increment count
count++;
i++;
} else {
// Decrement count
count--;
j++;
}
// Find maximum
ans = Math.max(ans, count);
}
return ans;
}
public static void main(String[] args) {
int[] arr = {900, 945, 955, 1100, 1500, 1800};
int[] dep = {920, 1200, 1130, 1150, 1900, 2000};
Solution sol = new Solution();
System.out.println("Minimum number of Platforms required: " + sol.findPlatform(arr, dep));
}
}
123456789101112131415161718192021222324252627282930313233
class Solution:
# To find number of platforms
def findPlatform(self, Arrival, Departure):
n = len(Arrival)
# Sort both arrival and departure arrays
Arrival.sort()
Departure.sort()
ans = 1
count = 1
i, j = 1, 0
# Iterate through the arrays
while i < n and j < n:
if Arrival[i] <= Departure[j]:
# Increment count
count += 1
i += 1
else:
# Decrement count
count -= 1
j += 1
# Find maximum
ans = max(ans, count)
return ans
# Test the solution
arr = [900, 945, 955, 1100, 1500, 1800]
dep = [920, 1200, 1130, 1150, 1900, 2000]
solution = Solution()
print("Minimum number of Platforms required:", solution.findPlatform(arr, dep))
12345678910111213141516171819202122232425262728293031323334353637
class Solution {
// To find number of platforms
findPlatform(Arrival, Departure) {
let n = Arrival.length;
// Sort both arrival and departure arrays
Arrival.sort((a, b) => a - b);
Departure.sort((a, b) => a - b);
let ans = 1;
let count = 1;
let i = 1, j = 0;
// Iterate through the arrays
while (i < n && j < n) {
if (Arrival[i] <= Departure[j]) {
// Increment count
count++;
i++;
} else {
// Decrement count
count--;
j++;
}
// Find maximum
ans = Math.max(ans, count);
}
return ans;
}
}
// Test the solution
let arr = [900, 945, 955, 1100, 1500, 1800];
let dep = [920, 1200, 1130, 1150, 1900, 2000];
let solution = new Solution();
console.log("Minimum number of Platforms required:", solution.findPlatform(arr, dep));