Bellman ford algorithm

Intuition:

The first thing that comes to mind when the requirement is to find shortest distance of all vertices from the source vertex S is Dijkstra's Algorithm. But this problem suggests that graphs can contain negative edges for which the Dijkstra's algorithm will fail.

To solve such issue, the Bellman Ford Algorithm will come in picture. It not only works when the graph contains negative edges, but also helps identify if the graph contains negative cycle (a cycle where sum of all weights is negative). The algorithm finds the minimum distance to reach any node by performing N-1 times Edge Relaxation (where N is the number of nodes in the graph). Though Bellman Ford Algorithm is more versatile, it is slower when compared to Dijkstra's Algorithm.

Edge Relaxation:

Consider an edge between node u and node v having a weight of wt as shown in the figure:
Consider the distance to reach node u and node v (via paths explored till now) be dist[u] and dist[v] respectively. If the distance taken to reach node v via some node u (dist[u] + wt) is smaller than the known distance to reach node v (dist[v]), then a shorter path to reach node v is found, which passes via node u. Thus, we update the distance to reach node v (dist[v]) to dist[u] + wt. This process of updating the distance is known as Edge Relaxation.

Why exactly N-1 iterations?

Longest Path in a Graph: The longest possible path without cycles in a graph with N nodes consists of (N-1) edges. And during each iteration, the Bellman-Ford algorithm updates the shortest path information for one more edge in the path.
Ensuring All Paths Are Considered: By repeating the relaxation process (N-1) times, the algorithm ensures that all vertices are updated based on paths that could extend up to (N-1) edges.

How to detect a negative cycle in the graph?

It is already known to us that if a graph has negative cycle, the edge relaxation can be done for an infinite number of times. But the algorithm suggests that all the edges will be relaxed after exactly (N-1) iterations.
Thus in order to check the existence of a negative cycle, an extra iteration can be performed to check if the edge relaxation is possible or not.
If in the extra iteration, the edge relaxation was possible, a negative cycle is confirmed in the graph.

Algorithm:

Set the distance to the starting node as 0 and to all other nodes as infinity.
On all the edges, perform Edge Relaxation for (N-1) times updating the distances of all nodes.
To detect if negative cycle exists, try performing edge relaxation on all the edges once more.
If for any edge, relaxation was possible, the graph contains a negative cycle.

Approach:

Initialize a distance array with a very large value (1e⁹) for all vertices. Set the distance of the source vertex to 0.
Perform edge relaxation on all edges for V-1 times, where V is the number of vertices i.e., check if the known distance to the destination vertex can be minimized by taking the edge. If yes, update the distance.
Perform an additional iteration over all edges to check for negative weight cycles. If any distance can still be minimized, a negative cycle exists in the graph, and the algorithm returns {-1}.
Return the distance array, which contains the shortest distances from the source to all other vertices, or {-1} if a negative cycle is detected.

Dry Run:

Solution:

#include <bits/stdc++.h>
using namespace std;

class Solution {
public:

    /* Function to implement 
    Bellman Ford Algorithm */
    vector<int> bellman_ford(int V, vector<vector<int>>& edges, 
                             int S) {
                                 
        // To store the distance
        vector<int> dist(V, 1e9);
        
        // Distane of source from itself is zero
        dist[S] = 0;
        
        // Repeat for V-1 times
        for(int i=0; i<V-1; i++) {
            
            // Iterate on all the edges
            for(auto it : edges) {
                
                int u = it[0]; // node 1
                int v = it[1]; // node 2
                int wt = it[2]; // edge weight
                
                // Edge relaxation
                if(dist[u] != 1e9 && 
                   dist[u] + wt < dist[v]) {
                       
                    // Updating the known distance
                    dist[v] = dist[u] + wt;
                }
            }
        }
        
        /* An extra relaxation to check if the 
        graph consists of a negative cycle */
        for(auto it : edges) {
            
            int u = it[0]; // node 1
            int v = it[1]; // node 2
            int wt = it[2]; // edge weight
            
            /* If edge relaxation is possible, 
            negative cycle exists */
            if(dist[u] != 1e9 && 
               dist[u] + wt < dist[v]) {
                   
                // Return {-1}
                return {-1};
            }
        }
        
        // Return the computed result
        return dist;
    }
};

int main() {
    int V = 6, S = 0;
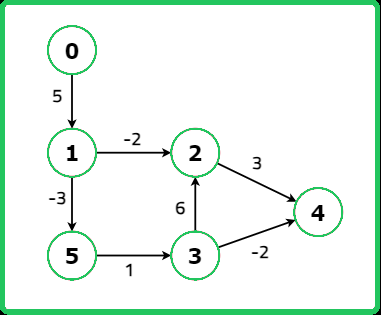
    vector<vector<int>> edges = {
        {3, 2, 6}, {5, 3, 1}, 
        {0, 1, 5}, {1, 5, -3}, 
        {1, 2, -2}, {3, 4, -2}, 
        {2, 4, 3}
    };
    
    /* Creating an instance of 
    Solution class */
    Solution sol; 
    
    /* Function call to implement 
    Bellman Ford Algorithm */
    vector<int> ans = sol.bellman_ford(V, edges, S);
    
    // Output
    if(ans == vector<int>(1, -1))
        cout << "The graph contains negative cycle.";
    else{
        cout << "The shortest distance from source is: ";
        for(int i=0; i < V; i++) {
            cout << ans[i] << " ";
        }
    }
    
    return 0;
}
import java.util.*;

class Solution {

    /* Function to implement 
    Bellman Ford Algorithm */
    public int[] bellman_ford(int V, 
        ArrayList<ArrayList<Integer>> edges, 
        int S) {
        
        // To store the distance
        int[] dist = new int[V];
        Arrays.fill(dist, (int) 1e9);
        
        // Distance of source from itself is zero
        dist[S] = 0;
        
        // Repeat for V-1 times
        for(int i = 0; i < V-1; i++) {
            
            // Iterate on all the edges
            for(ArrayList<Integer> it : edges) {
                
                int u = it.get(0); // node 1
                int v = it.get(1); // node 2
                int wt = it.get(2); // edge weight
                
                // Edge relaxation
                if(dist[u] != 1e9 && 
                   dist[u] + wt < dist[v]) {
                       
                    // Updating the known distance
                    dist[v] = dist[u] + wt;
                }
            }
        }
        
        /* An extra relaxation to check if the 
        graph consists of a negative cycle */
        for(ArrayList<Integer> it : edges) {
            
            int u = it.get(0); // node 1
            int v = it.get(1); // node 2
            int wt = it.get(2); // edge weight
            
            /* If edge relaxation is possible, 
            negative cycle exists */
            if(dist[u] != 1e9 && 
               dist[u] + wt < dist[v]) {
                   
                // Return {-1}
                return new int[]{-1};
            }
        }
        
        // Return the computed result
        return dist;
    }

    public static void main(String[] args) {
        int V = 6, S = 0;
        ArrayList<ArrayList<Integer>> edges = new ArrayList<>();
        edges.add(new ArrayList<>(Arrays.asList(3, 2, 6)));
        edges.add(new ArrayList<>(Arrays.asList(5, 3, 1)));
        edges.add(new ArrayList<>(Arrays.asList(0, 1, 5)));
        edges.add(new ArrayList<>(Arrays.asList(1, 5, -3)));
        edges.add(new ArrayList<>(Arrays.asList(1, 2, -2)));
        edges.add(new ArrayList<>(Arrays.asList(3, 4, -2)));
        edges.add(new ArrayList<>(Arrays.asList(2, 4, 3)));
        
        /* Creating an instance of 
        Solution class */
        Solution sol = new Solution();
        
        /* Function call to implement 
        Bellman Ford Algorithm */
        int[] ans = sol.bellman_ford(V, edges, S);
        
        // Output
        if(ans.length == 1 && ans[0] == -1)
            System.out.println("The graph contains negative cycle.");
        else{
            System.out.print("The shortest distance from source is: ");
            for(int i = 0; i < V; i++) {
                System.out.print(ans[i] + " ");
            }
        }
    }
}
class Solution:

    # Function to implement 
    # Bellman Ford Algorithm
    def bellman_ford(self, V, edges, S):
        
        # To store the distance
        dist = [int(1e9)] * V
        
        # Distance of source from itself is zero
        dist[S] = 0
        
        # Repeat for V-1 times
        for _ in range(V-1):
            
            # Iterate on all the edges
            for u, v, wt in edges:
                
                # Edge relaxation
                if (dist[u] != int(1e9) and 
                    dist[u] + wt < dist[v]):
                       
                    # Updating the known distance
                    dist[v] = dist[u] + wt
        
        # An extra relaxation to check if the 
        # graph consists of a negative cycle
        for u, v, wt in edges:
            
            # If edge relaxation is possible, 
            # negative cycle exists
            if (dist[u] != int(1e9) and 
                dist[u] + wt < dist[v]):
                   
                # Return [-1]
                return [-1]
        
        # Return the computed result
        return dist


if __name__ == "__main__":
    V, S = 6, 0
    edges = [
        [3, 2, 6], [5, 3, 1], 
        [0, 1, 5], [1, 5, -3], 
        [1, 2, -2], [3, 4, -2], 
        [2, 4, 3]
    ]
    
    # Creating an instance of 
    # Solution class
    sol = Solution()
    
    # Function call to implement 
    # Bellman Ford Algorithm
    ans = sol.bellman_ford(V, edges, S)
    
    # Output
    if ans == [-1]:
        print("The graph contains negative cycle.")
    else:
        print("The shortest distance from source is: ", end=" ")
        for d in ans:
            print(d, end=" ")
class Solution {

    /* Function to implement 
    Bellman Ford Algorithm */
    bellman_ford(V, edges, S) {
        
        // To store the distance
        let dist = new Array(V).fill(1e9);
        
        // Distance of source from itself is zero
        dist[S] = 0;
        
        // Repeat for V-1 times
        for (let i = 0; i < V-1; i++) {
            
            // Iterate on all the edges
            for (let it of edges) {
                
                let u = it[0]; // node 1
                let v = it[1]; // node 2
                let wt = it[2]; // edge weight
                
                // Edge relaxation
                if (dist[u] != 1e9 && dist[u] + wt < dist[v]) {
                       
                    // Updating the known distance
                    dist[v] = dist[u] + wt;
                }
            }
        }
        
        /* An extra relaxation to check if the 
        graph consists of a negative cycle */
        for (let it of edges) {
            
            let u = it[0]; // node 1
            let v = it[1]; // node 2
            let wt = it[2]; // edge weight
            
            /* If edge relaxation is possible, 
            negative cycle exists */
            if (dist[u] != 1e9 && dist[u] + wt < dist[v]) {
                   
                // Return [-1]
                return [-1];
            }
        }
        
        // Return the computed result
        return dist;
    }
}

// Main function
let V = 6, S = 0;
let edges = [
    [3, 2, 6], [5, 3, 1], 
    [0, 1, 5], [1, 5, -3], 
    [1, 2, -2], [3, 4, -2], 
    [2, 4, 3]
];

/* Creating an instance of 
Solution class */
let sol = new Solution();

/* Function call to implement 
Bellman Ford Algorithm */
let ans = sol.bellman_ford(V, edges, S);

// Output
if (ans.length === 1 && ans[0] === -1)
    console.log("The graph contains negative cycle.");
else {
    console.log("The shortest distance from source is: ", ans.join(" "));
}

Complexity Analysis:

Time Complexity: O(V*E)
All the E edges are relaxed for a total of V-1 times. And an extra iteration is performed to detect negative cycle, making the algorithm take O(V*E) time.

Space Complexity: O(V)
The distance array takes O(V) time.

Problem List

Examples:

Constraints

Hints

Company Tags

Editorial

Intuition:

Edge Relaxation:

Why exactly N-1 iterations?

How to detect a negative cycle in the graph?

Algorithm:

Approach:

Dry Run:

Solution:

Complexity Analysis:

Frequently Occurring Doubts

Interview Followup Questions

Notes

Code